An object with a mass of #19 kg# is on a ramp at an incline of #pi/12 #. If the object is being pushed up the ramp with a force of # 6 N#, what is the minimum coefficient of static friction needed for the object to remain put?
1 Answer
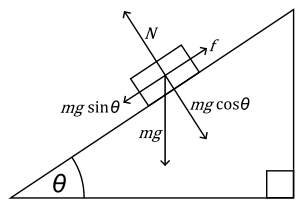
Given that
-
the angle of inclination of the ramp
#theta=pi/12# . -
the mass of the object kept on the ramp
#m=19kg# . -
the object being pushed up by a force
#F=6N#
Now
-
the component of gravitational force acting on the object against applied force along the ramp
#=mgsintheta# -
normal reaction acting on the object
#mgcostheta# -
upward static frictional force acting on the object
#f=mumgcostheta# , where#mu# is the coefficient of static friction.
Cinsidering the equilibrium of forces we get following relation

