An object with a mass of 2 kg is on a ramp at an incline of pi/12 . If the object is being pushed up the ramp with a force of 8 N, what is the minimum coefficient of static friction needed for the object to remain put?
1 Answer
Jun 3, 2018
Explanation:
we can write
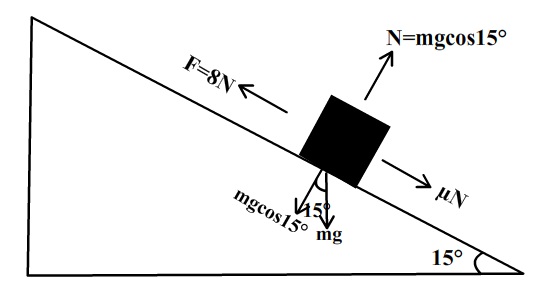
Now please consider the image and look at the free body diagram and the forces acting on it.
Thus for the object to be put,
as
after calculation
Hence coefficient of static friction is

