Question

An object with a mass of `4 kg` is lying still on a surface and is compressing a horizontal spring by `1/4 m`. If the spring's constant is `6 (kg)/s^2`, what is the minimum value of the surface's coefficient of static friction?

Answer 1

`mu_s~~0.04`

Explanation:

We will solve this first by setting up a force diagram and writing out sum of forces statements.

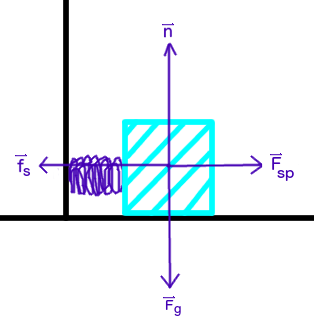
Where `vecn` is the normal force, `vecF_g` is the force of gravity, `vecF_(sp)` is the force of the spring, and `vecf_s` is the force of static friction. I will define rightward as positive.

Statements of the net force:

`sumF_x=vecF_(sp)-vecf_s=mveca_x`

`sumF_y=vecn-vecF_g=mveca_y`

The object is not moving, and experiences no net acceleration in either `x`- or `y`-direction.

`sumF_x=vecF_(sp)-vecf_s=cancel(mveca_x)=vec0`

`sumF_y=vecn-vecF_g=cancel(mveca_y)=vec0`

We can rearrange these statements to find:

`vecF_(sp)=vecf_s`

`vecn=vecF_g`

Where `vecF_g=mg`

The equation for the frictional force is `vecf=muvecn`. Therefore, we have:

`vecF_(sp)=mumg`

The equation for the spring force is given by Hooke's law as `vecF_(sp)=k(Deltas)`, where `k` is the spring constant and `Deltas` is the displacement from equilibrium (how far the spring is stretched or compressed).

`k(Deltas)=mumg`

Solving for `mu`, the coefficient of friction:

`mu=(k(Deltas))/(mg)`

Using our known values, we can calculuate `mu`:

`mu=((6N/m)(1/4m))/(4kg*9.8m/s^2)`

`mu=0.038...~~0.04`

Therefore, the minimum coefficient of static friction to keep the object still is `~~0.04`.