An object with a mass of #5 kg# is on a ramp at an incline of #pi/8 #. If the object is being pushed up the ramp with a force of # 2 N#, what is the minimum coefficient of static friction needed for the object to remain put?

Question

1482 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-30T10:58:17

#color(blue)(0.37)color(white)(8888)# 2 d.p.

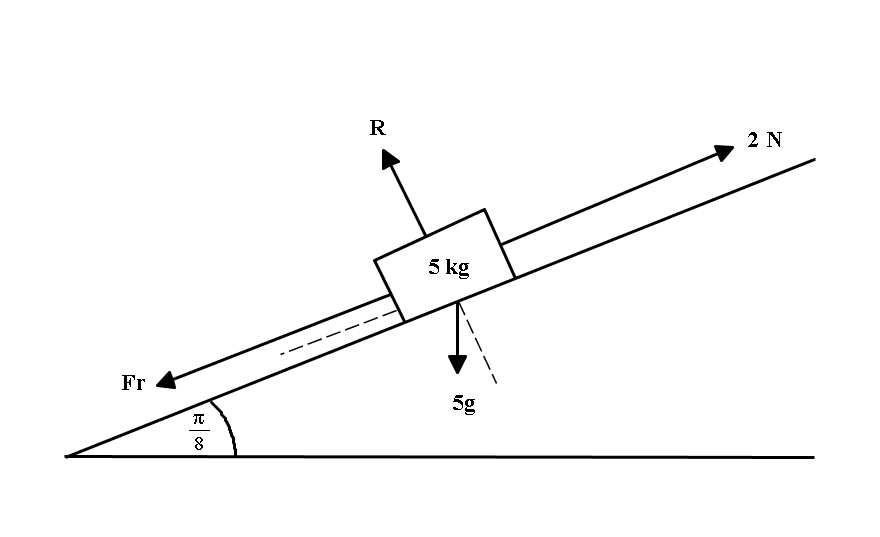
enter image source here

Since the #bb(2 N)# force is acting upwards the frictional force #bb(Fr)# is acting in the opposite direction.

For the body to remain static, we have:

#Fr=muR#

Where #mu# is the coefficient of friction.

Resolving forces perpendicular to the plane:

#R=5gcos(pi/8)#

Resolving forces horizontal to the plane:

#Fr=5gsin(pi/8)-2N#

Substituting these two equations into# \ \ \ \ \Fr=muR#:

#5gsin(pi/8)-2=mu*5gcos(pi/8)#

#:.#

#mu=(5gsin(pi/8)-2)/(5gcos(pi/8))#

Taking #g=9.81#

#mu=(5*(9.81)sin(pi/8)-2)/(5*(9.81)cos(pi/8))=0.3700793240N#

#mu=0.37# 2 d.p.