An object with a mass of #5 kg# is on a surface with a kinetic friction coefficient of # 4 #. How much force is necessary to accelerate the object horizontally at # 17 m/s^2#?

1 Answer
Narad T.
Apr 9, 2017

The force is #=281N#

Explanation:

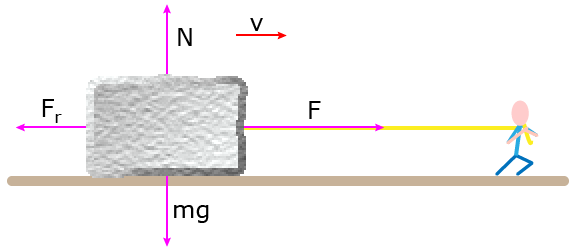
enter image source here

The frictional force is

#F_r=mu_k*N#

The normal force is #N=mg#

So,

#F_r=mu_k*mg#

Resolving in the horizontal direction #rarr^+#

We apply Newton's second Law

#F-F_r=ma#

So,

#F=F_r+ma#

#F=mu_kmg+ma#

#=m(mu_kg+a)#

#=5(4*9.8+17)#

#=5*56.2=281N#

Related questions
See all questions in Frictional Forces
Impact of this question
1484 views around the world
You can reuse this answer
Creative Commons License