Question

An object with a mass of `6 kg` is on a plane with an incline of `- pi/6`. If it takes `15 N` to start pushing the object down the plane and `6 N` to keep pushing it, what are the coefficients of static and kinetic friction?

Answer 1

`mu_s~~0.872`
`mu_k~~0.695`

Explanation:

A force diagram:

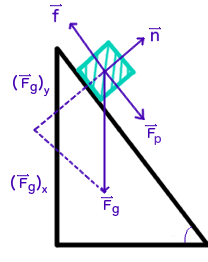
where `vecn` is the normal force, `vecF_G` is the force of gravity broken into its respective parallel and perpendicular components, `vecF_p` is the pushing force that is applied to the object, and `vecf` generically represents the force of friction, either static or kinetic.

Note that I have defined down the ramp as the positive direction.

this determines whether I will designate forces as being "positive" or "negative"

Let's begin with static friction. We know that in order for the object to begin to move down the ramp, we must apply a great enough pushing force to overcome `f_(smax)`, the maximum force of static friction. I will simply write `f_s` from now on.

We should take inventory of the forces:

`(F_(n e t))_x=sumF_x=F_p+(F_G)_x-f_s=ma_x`

`(F_(n e t))_y=sumF_y=n-(F_G)_y=ma_y`

Since the object is not accelerating vertically (not moving up and down relative to the surface of the inclined plane), we know that `a_y=0`. Because it is maximum static friction in question, until this force is overcome, the system is in static equilibrium: forces are being applied to the object but they are not causing a net acceleration and so the object remains at rest.

And so we have:

`F_p+(F_G)_x-f_s=0`

`n-(F_G)_y=0`

We also know that `f_s=mu_sn` (the "fun" equation), and by basic trigonometry, `(F_G)_x=mgsintheta` and `(F_G)_y=mgcostheta`. Therefore:

`n=mgcostheta`

`=>F_P+mgsintheta=mgcostheta*mu_s`

Solving for `mu_s`

`mu_s=(F_P+mgsintheta)/(mgcostheta)`

`=(15N+(6kg)(9.81m/s^2)sin(pi/6))/((6kg)(9.81m/s^2)cos(pi/6))`

`~~0.872`

For kinetic friction, we assume that when we do surpass `f_(smax)`, the object is not accelerating, and is therefore now in dynamic equilibrium. Therefore, we have:

`(F_(n e t))_x=sumF_x=F_p+(F_G)_x-f_k=0`

`(F_(n e t))_y=sumF_y=n-(F_G)_y=0`

As above, we use trigonometry and `f_k=mu_kn` to solve for `mu_k`:

`=>mu_k=(F_p+mgsintheta)/(mgcostheta)`

`=(6N+(6kg)(9.81m/s^2)sin(pi/6))/((6kg)(9.81m/s^2)cos(pi/6))`

`~~0.695`

We find that `mu_k < mu_s` which is expected. Also note that coefficients of friction have no units; they are dimensionless.