Question

An object with a mass of `7 kg` is on a surface with a kinetic friction coefficient of `8`. How much force is necessary to accelerate the object horizontally at `4 m/s^2`?

Answer 1

Let us apply Newton's Laws to solve this problem.

Explanation:

According to Newton's 2nd Law of Motion (`F=ma`), to get an acceleration of 4 `"m/s"^2`, we need a force:

`F = m cdot a = 7 " kg" cdot 4 " m/s"^2 = 28 " N"`

This would be the force necessary to move the body if there were not any other forces (as friction). However, in our case, a stronger force is required to compensate friction.
So, let us take 28 N as net force.

Now, we are going to find friction force. This equals to:

`F_"friction" = mu cdot N = mu cdot m g = 8 cdot 7 " kg" cdot 9,8 " m/s"^2 =`
`= 548,8 " N"`

So net force will be:

`F_"net" = F_"applied" - F_"friction" = 28 " N"`

We can see next picture to understand it better:

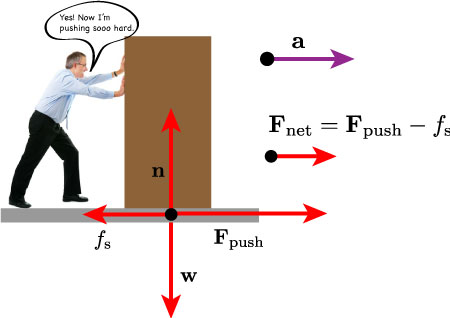
Now, having `F_"net"` and `F_"friction"`, let us find `F_"applied"`:

`F_"applied" = F_"net" + F_"friction" = 28 " N" + 548,8 " N" = 576,8 " N"`