Question

An object with a mass of `8 kg` is on a plane with an incline of `- pi/3`. If it takes `16 N` to start pushing the object down the plane and `15 N` to keep pushing it, what are the coefficients of static and kinetic friction?

Answer 1

`mu_s<=2.13, mu_k~~2.11`

Explanation:

To determine the coefficients of (maximum) static and kinetic friction, we can set up a force diagram and take inventory of all of the forces acting on the object.

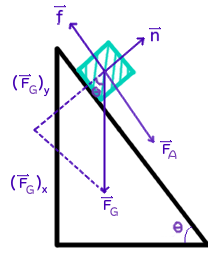
where `vecn` is the normal force, `vecF_A` is the applied (pushing) force, `vecf` is the force of friction, and `vecF_G` is the force of gravity, decomposed into its parallel and perpendicular components

Since we're pushing the object down the plane, I'm going to define down the ramp as the positive direction. This choice is generally up to you.

Therefore, we have:

`color(darkblue)((F_x)_(n et)=sumF_x=F_A+(F_G)_x-f=ma_x)`

`color(darkblue)((F_y)_(n et)=sumF_y=n-(F_G)_y=ma_y)`

We are given the following information:

• `|->m=8"kg"`
• `|->theta=-(pi)/3->60^o`
• `|->F_A " to start moving" = 16"N"`
• `|->F_A " to keep moving" = 15"N"`

We'll begin with the coefficient of static friction. The force of static friction is given by:

`color(darkblue)(vecf_(s"max")=mu_svecn)`

We are told that it takes `16"N"` to get the object to start moving, which we interpret as a minimum of `16"N"`. Therefore, there is just enough force applied to move the object, and so there is no acceleration. This means the object is in a state of dynamic equilibrium.

• This is actually true for both the parallel (x, horizontal) and perpendicular (y, vertical) directions, as the object does not move up and down, meaning that the perpendicular component of gravity is equal and opposite to the normal force.

`color(darkblue)(F_(x" net")=sumF_x=F_A+F_(Gx)-f_(s "max" )=0)`

`color(darkblue)(F_(y" net")=sumF_y=n-F_(Gy)=0)`

Hence, we now have:

`F_A+F_(Gx)=f_(s"max")`

`n=F_(Gy)`

Using trigonometry, we see that:

`sin(theta)="opposite"/"hypotenuse"`

`=>sin(theta)=(F_G)_x/F_G`

`=>color(blue)((F_G)_x=F_Gsin(theta))`

Similarly, we find that `color(blue)((F_G)_y=F_Gcos(theta))`

We also know that `F_G=mg`, so:

`F_A+mgsin(theta)=mu_(s"max")n`

`=>F_A+mgsin(theta)=mu_(s"max")mgcos(theta)`

Solving for `mu_s`:

`color(blue)(mu_(s"max")=(F_A+mgsin(theta))/(mgcos(theta)))`

Substituting in our known values:

`mu_(s"max")=((16"N")+(8"kg")(9.81"m"//"s"^2)sin(60^o))/((8"kg")(9.81"m"//"s"^2)cos(60^o))`

`=2.1340`

`~~color(blue)(2.13)`

• Therefore, the coefficient of maximum static friction is `~~color(dark blue)(2.13)`, and so the coefficient of static friction is `>=2.13`.

For the coefficient of kinetic friction, we do much of the same, including the assumption of dynamic equilibrium.

`mu_k=(F_A+mgsin(theta))/(mgcos(theta))`

`=((15"N")+(8"kg")(9.81"m"//"s"^2)sin(60^o))/((8"kg")(9.81"m"//"s"^2)cos(60^o))`

`=2.114`

`~~color(blue)(2.11)`

• Therefore, the coefficient of kinetic friction is `~~2.11`.

We would expect `mu_s>mu_k`, which works out here, even if slightly.