An object with a mass of #8 kg# is on a plane with an incline of # - pi/8 #. If it takes #4 N# to start pushing the object down the plane and #1 N# to keep pushing it, what are the coefficients of static and kinetic friction?
1 Answer
The static coefficient of friction is
The kinetic coefficient of friction is
Explanation:
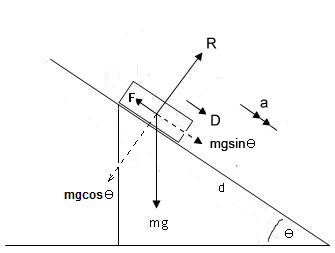
For our diagram,
If we apply Newton's Second Law up perpendicular to the plane we get:
#R-mgcostheta=0#
#:. R=8gcos(pi/8) \ \ N#
Initially it takes
# D+mgsin theta -F = 0 #
# :. F = 4+8gsin (pi/8) \ \ N#
And the friction is related to the Reaction (Normal) Force by
# F = mu R => 4+8gsin (pi/8) = mu (8gcos(pi/8)) #
# :. mu = (4+8gsin (pi/8))/(8gcos(pi/8)) #
# :. mu = 0.469437 ... #
Once the object is moving the driving force is reduced from
# D+mgsin theta -F = 0 #
# :. F = 1+8gsin (pi/8) \ \ N#
And the friction is related to the Reaction (Normal) Force by
# F = mu R => 1+8gsin (pi/8) = mu (8gcos(pi/8)) #
# :. mu = (1+8gsin (pi/8))/(8gcos(pi/8)) #
# :. mu = 0.428019 ... #
So the static coefficient of friction is
the kinetic coefficient of friction is

