Boxes A and B are attached by a rope. They are on a platform floor attached to a helicopter that is falling. Box A is pulled #35^@# to the surface. What is the tension between A and B as they slide horizontally on the platform?
Box A (#12.0kg# ) and B (#7.0kg# ) are attached by a rope. They are on a platform floor attached to a helicopter that is falling at a rate of #2.5m/s^2# . Box A is pulled with a force of #42N# , #35^@# to the surface. The coefficient of friction for both A and B against the floor is #mu_k=0.20# . What is the tension between A and B as they slide horizontally on the platform?
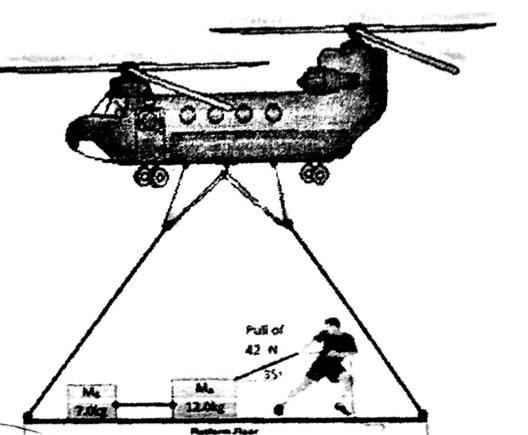
Box A (

1 Answer
Explanation:
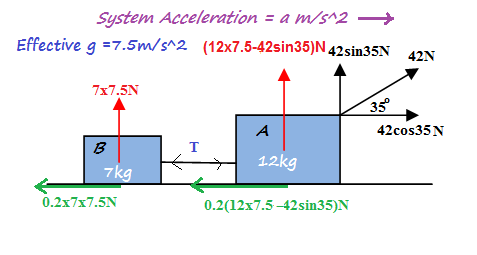
As the Helicopter is falling with acceleration
Given
-
#m_A->"Mass of box A" =12kg# -
#m_B->"Mass of box B" =7kg# -
#mu_k->"Coefficient of kinetic friction " =0.2# -
#"Applied force on A"=42N ," acting " 35^@ "with horizontal"# -
#"Horizontal component of 42N"=42cos35N# -
#"Vertictal component of 42N"=42sin35N#
Let the combined system is moving with acceleration
Then considering forces acting on 7 kg box (B ) we can write
Dividing both sides by 7
Again considering forces acting on12kg box (A ) we can write
Dividing both sides by 12 we get
Now subtracting (2) from (1) we get

