By considering the roots of #z^5 =1#, how do you show that cos(2π/5) + cos(4π/5) + cos(6π/5) + cos(8π/5) = -1?
1 Answer
Please see below.
Explanation:
As
According to De-Moivre's theorem
and these five roots, when graphed on the complex plane, are equally spaced around a circle of unit radius as shown below.
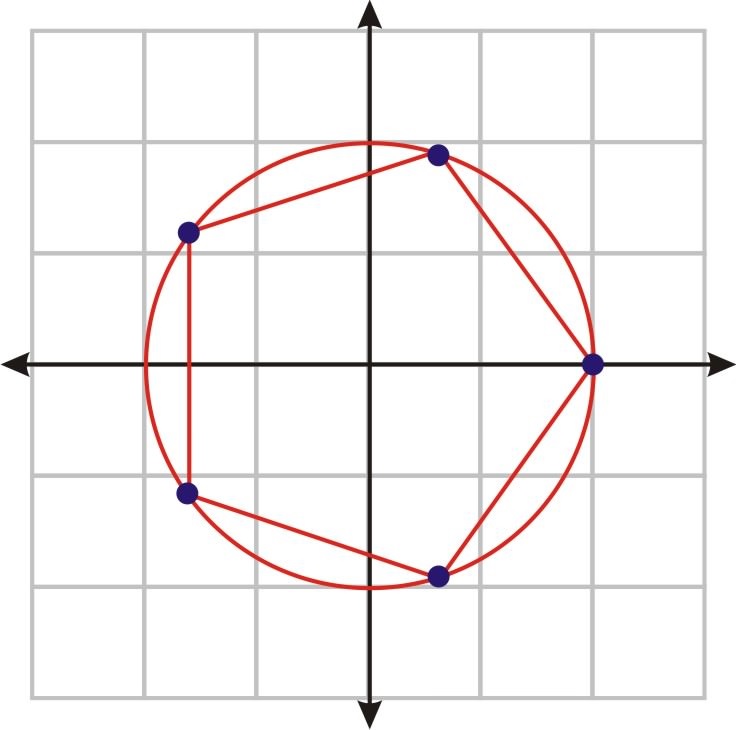
and it is apparent that their sum will be zero.
As such comparing real and imaginary parts we should have
and
i.e.
and
