Can anybody help me with this optimization problem?
A rectangle has one vertex at the origin, one of the x-axis, one on the y-axis, and one on the graph of #y=sqrt(4-x)#
What is the largest the rectangle can have, and what are its dimensions?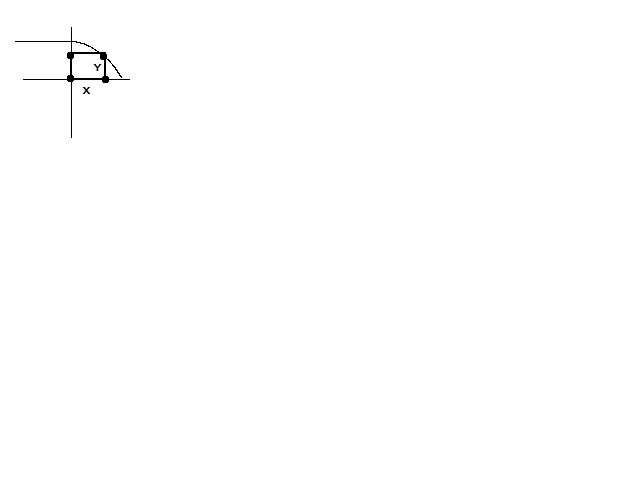
This is everything I've figured out so far. I'm guessing that
#A=xy#
and
#A=x(sqrt(4-x))#
But I don't know how to continue
Thank you!
A rectangle has one vertex at the origin, one of the x-axis, one on the y-axis, and one on the graph of
What is the largest the rectangle can have, and what are its dimensions?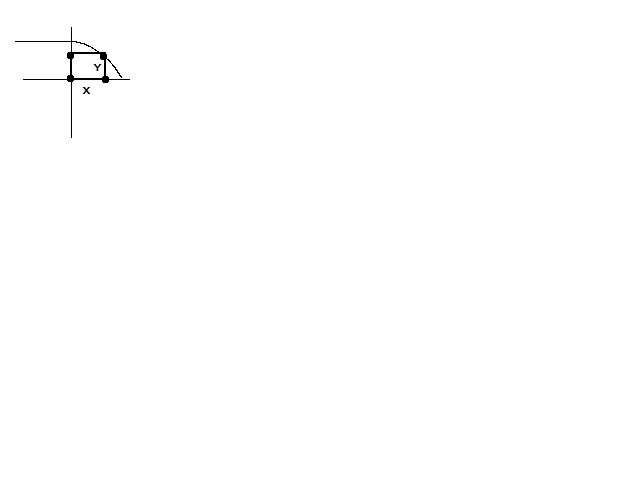
This is everything I've figured out so far. I'm guessing that
and
But I don't know how to continue
Thank you!
1 Answer
Dimensions of largest rectangle are
Explanation:
By largest one means largest area.
As area is given by
it will be maximized when
As
=
and
or
=
=
and
or
Dimensions of largest rectangle are
and its area is
Below is graph of
graph{xsqrt(4-x) [-3.063, 6.937, -1.12, 3.88]}
