Question

Can anyone help confirm the answer I have to these 3 questions?

1) 10.0 km
2) Magnitude: 253km/h Direction: N(9)E
3) Northwest and 2.6 minutes

Answer 1

Please see below. I have somewhat different results, but you can follow the process and check.

Explanation:

(1) As hiker moves `6.0` km. east and then `8.0` km. north, his movement can be depicted in following figure.

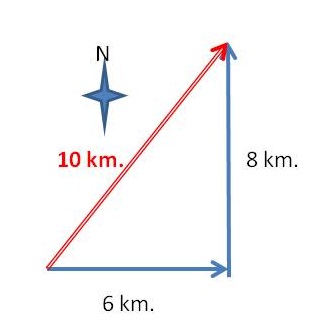
Now as p Pythagoras theorem, his movement is `sqrt(6^2+8^2)=sqrt(36+64)=sqrt100=10` km.

(2) Again the movement of plane is shown in following diagram. The plane travels north at `250` `(km.)/(hr.)` for two hour and is then `500` `km.` north, but is displaced `40` `km.` to southwest.

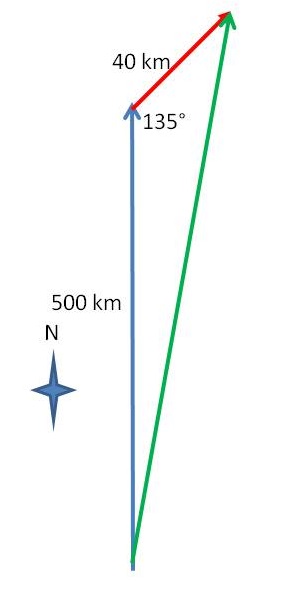
The resultant displacement is given by solution of triangle for third side i.e. `sqrt(500^2+40^2-2xx40xx500xxcos135^@)`

= `sqrt(250000+1600+40000xx0.7071)`

= `sqrt279884=529.04`

and resultant velocity is `529.04/2=264.52` `(km)/(hr.)` towards east at an angle `theta` from north given by `sintheta/40=sin135^@/529.04`

i.e. `sintheta=(40xx0.7071)/529.04` and `theta=3.065^@`

(3) As Andy can paddle canoe at `1.2` `m/s`, he covers `200m` in `200/1.2` seconds. During this period river current sends him `200/1.2xx0,4=200/3m` east.

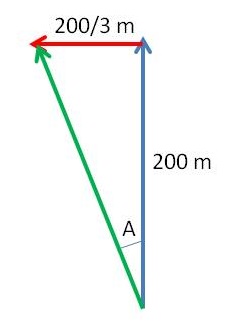
As such he should paddle towards west and as distance covered is

`sqrt(200^2+(200/3)^2)=200/3sqrt10=210.82`

and time taken is `210.82/1.2=175.7` second or `175.7/60=2.93` minutes.