Can someone please thoroughly explain titrations and their graphs? Thank you!
What is the purpose of a titration? What/where is the equivalence point? Half-equivalence point? Where are those points located on a titration graph? And is there any other information that you think is helpful/important?
What is the purpose of a titration? What/where is the equivalence point? Half-equivalence point? Where are those points located on a titration graph? And is there any other information that you think is helpful/important?
2 Answers
Please see explanation. I don't know about half-equivilance points / graphs though.
Explanation:
A titration can be performed in order to determine the concentration of an acid or a base by neutralizing it with another acid or base which you know the concentration of.
This is useful because, if you had HCl with an unknown concentration, it can either scar you for life when you touch it, or irritate you for a while. To be safe, we can use titration to determine its concentration.
If you are doing a lab with titration, it must be very precise. In general, you place acid-base indicator such as phenolphthalein to find out when the equivalence point is reached. This is the point where the indicator has switched colours, indicating the volume of the acid or base that was used to neutralize the acid or base in question. Using the equation
Take the titration curve for
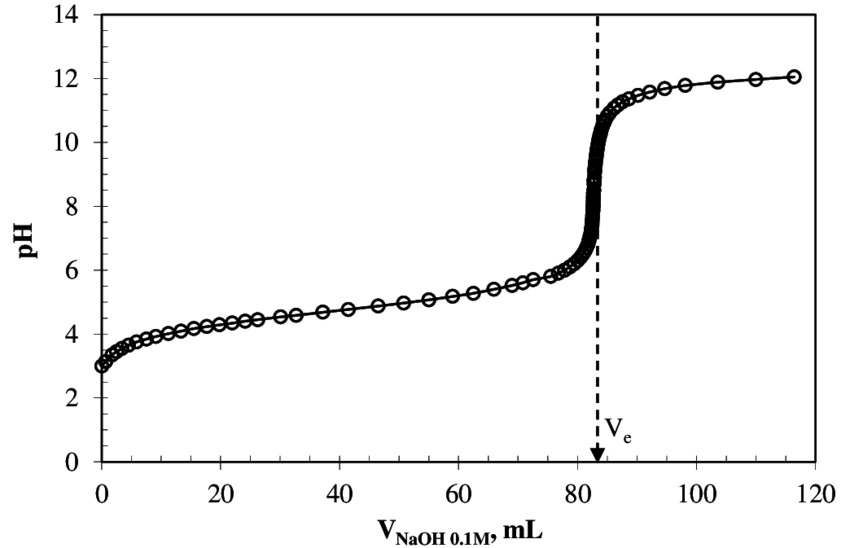
The rest of this answer will assume strong base is added to weak acid. However, strong acid could just as easily be added to weak base, and the above graph would be flipped horizontally.
Let's say you know what your acid is already. Then the point of a titration is to:
- verify the concentration of your base (whose concentration might be hard to determine if the solid used to make it is hygroscopic---that is, if it absorbs moisture in the air).
- to check the
#"pKa"# of your acid.
That is done by knowing the mass you used to make your acid solution, so that you can calculate its starting concentration with a good amount of certainty.
If you do NOT know what your acid is, then the titration is done to determine its
A common lab procedure is to first use a known acid (your primary standard) that you've prepared to determine the concentration of your secondary standard (in this case,
BUFFER REGION
The side of the graph before the steep rise is the buffer region. It is where your weak acid, while being neutralized, is in the presence of its conjugate weak base (which is being produced as the weak acid is being neutralized).
It is here that the Henderson-Hasselbalch equation can be used.
EQUIVALENCE POINT
The equivalence point is the spot indicated on the graph by
(That is, it is the volume of titrant that contains the exact number of mols you need to react with all of what you are titrating.)
Once you make it past here, you're at a part of the titration where you have only the weak conjugate base and any extra
HALF-EQUIVALENCE POINT
The half-equivalence point is what you'll need to locate to find the
In other words, it is at
#"pH" = "pKa" + log\frac(["A"^(-)])(["HA"])#
Of course, the Henderson-Hasselbalch equation only works in the BUFFER REGION... at the equivalence point, the logarithm tends to infinity...


