Carbon-14 has a half-life of 5770 years. If a fossil is 23,080 years old and it has 3 Kg of Carbon-14, how much carbon-14 did it originally have?
1 Answer
Explanation:
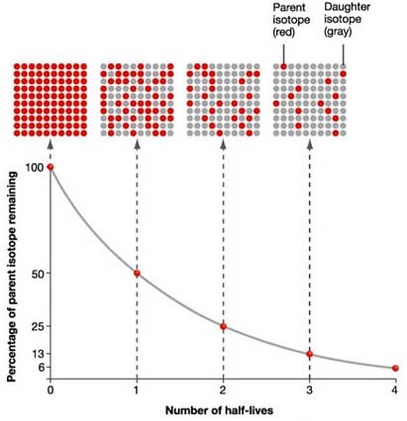
The nuclear half-life is simply the time needed for half of the atoms present in a sample of a radioactive substance to undergo radioactive decay.
In your case, carbon-14 is said to have a half-life of
Now, if
An interesting technique to use here is to backtrack from current time, when the sample is down to
You can thus say that
#2 xx "3 kg" = "6 kg"#
How about
#2 xx "5770 years" = "11,540 years ago"# The mass of the sample was
#2 xx "6 kg" = "12 kg"#
How about
#3 xx "5770 years" = "17,310 years ago"# The mass of the sample was
#2 xx "12 kg" = "24 kg"#
Finally, how about
#4 xx "5770 years" = "23,080 years ago"# The mass of the sample was
#2 xx "24 kg" = "48 kg"#
Therefore,
When the values don't allow for such simple calculations, you can use the equation
#color(blue)(|bar(ul(color(white)(a/a)"A"_t = "A"_0 * 1/2^ncolor(white)(a/a)|)))#
Here
In your case, you have
#n = ("23,080" color(red)(cancel(color(black)("years"))))/(5770color(red)(cancel(color(black)("years")))) = 4#
You will thus have
#"A"_0 = "A"_t * 2^4#
#"A"_0 = "3 kg" * 2^4 = color(green)(|bar(ul(color(white)(a/a)color(black)("48 kg")color(white)(a/a)|)))#