Derive the sine sum formula using the geometrical construction given in the figure?

Question

2409 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-08-25T20:56:37

#sin(alpha+beta)=sin(alpha)cos(beta)+cos(alpha)sin(beta)#

First, construct two additional lines and label the intersections/vertices as follows:

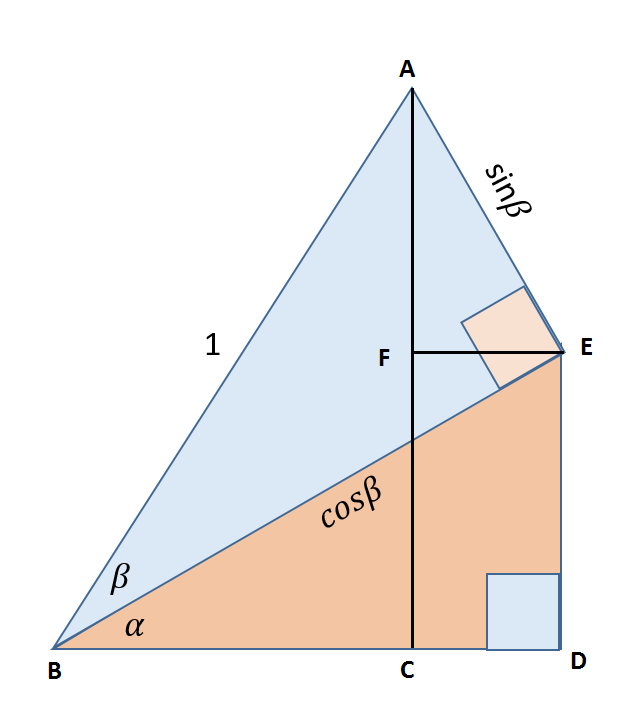
enter image source here

Proceeding, note that from the right triangle #triangleACB#, we have
#sin(alpha+beta) = (AC)/(AB) = (AC)/1=AC#

Then, it remains to calculate #AC#. To do so, we will calculate #AF# and #FC# separately, and then add them together.

From the right triangle #triangleBDE#, we have
#sin(alpha) = (ED)/(BE) = (ED)/cos(beta)#

#=> ED = sin(alpha)cos(beta)#

#=> FC = ED = sin(alpha)cos(beta)#

Next, as the sum of the angle of #triangleBDE# is #pi#, we have #angleBED = pi-pi/2-alpha = pi/2-alpha#.

As #angleAEB=pi/2#, this gives #angleAED = pi/2+(pi/2-alpha)=pi-alpha#.

Then, as #angleFED = pi/2# by construction, we have #angleAEF = pi-alpha-pi/2 = pi/2-alpha#.

Looking at the right triangle #triangleAFE#, then, we can calculate #angleFAE# as
#angleFAE = pi-pi/2-(pi/2-alpha) = alpha#.

Calculating the cosine of that angle, we obtain
#cos(alpha) = (AF)/(AE) = (AF)/sin(beta)#

#=> AF = cos(alpha)sin(beta)#

Putting these together, we get our final result:

#sin(alpha+beta) = AC#

#=FC+AF#

#=sin(alpha)cos(beta)+cos(alpha)sin(beta)#