Determine #f#, #c# and #p# in these reactions (Gibbs' Phase Rule)?
In reactions:
a) FeO(g)+CO(g)-> Fe(s)+(CO2)g
b) water solution of AlCl3
determine #f# , #c# and #p# based on Gibb's phase rule where #f# is the number of degrees of freedom, #c# is the number of components and #p# is the number of phases in thermodynamic equilibrium with each other.
In reactions:
a) FeO(g)+CO(g)-> Fe(s)+(CO2)g
b) water solution of AlCl3
determine
1 Answer
The Gibbs' Phase rule is:
#f = 2 + c_i - p#
#c_i = c - r - a# where:
#f# is the number of degrees of freedom (how many independent intensive variables can be varied without affecting other thermodynamic variables).#c_i# is the number of chemically independent components in the system.#c# is the number of components in the system, ignoring their chemical independence.#p# is the number of phases.#r# is the number of reactions.#a# is the number of additional restrictions (e.g. charge balance).
If we assume that there is no further reaction occurring, then there are
The number of phases,
Therefore,
An aqueous solution of
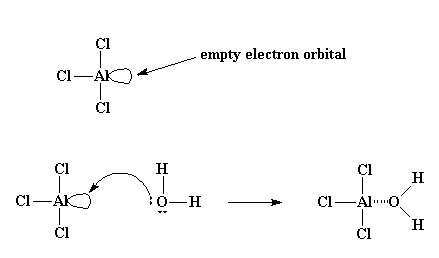
CASE I
If we assume a sufficiently dilute solution, we can pretend that
#"AlCl"_3(aq) + 3"H"_2"O"(l) -> "Al"("OH")_3(s) + 3"HCl"(g)#
We include these non-independent components:
#"H"_2"O"(l)# #"OH"^(-)(aq)# #"H"^(+)(aq)# #"Al"("OH")_3(s)# #"HCl"(g)#
With the water ions in solution, we have
The number of phases is
CASE II
If the solution is NOT sufficiently dilute, and we assume a reaction DOES occur (to completion), then we must include all of these non-independent components, assuming excess water (but neglecting the coordination of water to
#"H"_2"O"(l)# #"OH"^(-)(aq)# #"H"^(+)(aq)# #"Al"("OH")_3(s)# #"HCl"(g)#
I will assume case II, which omits the water association reaction and omits the
This gives that
You should see that in both cases, we get the same number for
If the reaction is in a closed system, then we again have three phases (liquid, solid, and gas), so
#color(blue)(f) = 2 + c_i - p#
#= 2 + 3 - 3 = color(blue)(bb(2))#
which means you can change the temperature and pressure (two natural variables) a little and not move off the phase equilibrium you establish, assuming a closed system.

