Draw #BF_3# and assign a point group. How many degrees of vibrational freedom does the molecule have?
1 Answer
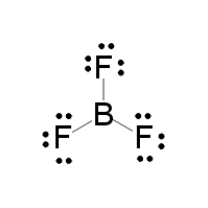
LEWIS STRUCTURE
#7 xx 3# valence electrons from the fluorines#3# valence electrons from the boron
And thus, using
POINT GROUP
Now, to get the point group, we consider the general symmetry operations:
#hatC_n# : Proper RotationRotate the molecule
#360^@/n# degrees, so that it returns to an orientation indistinguishable from the previous. For instance,#hatC_3# is a#120^@# rotation (#360^@/3 = 120^@# ).
#hatsigma# : Reflection PlaneThere exist
#hatsigma_h# ,#hatsigma_v# , and#hatsigma_d# (horizontal, vertical, dihedral).
- The
#sigma_h# symmetry element is perpendicular to the#C_n# of the highest#n# (the principal rotation axis).- The
#sigma_v# symmetry element is colinear with the#C_n# of the highest#n# , but perpendicular to any present#sigma_h# - The
#sigma_d# symmetry element bisects and is perpendicular to two#C_2# axes that are coplanar with a#sigma_h# .
#hatS_n# : Improper RotationThis is basically
#hatC_nhatsigma_h# or#hatsigma_hhatC_n# in one. Rotate about the axis, then reflect through the plane perpendicular to that axis. If you know how to use#hatC_n# and#hatsigma_h# , you know how this works.
#hati# : InversionThe easiest way I can describe this is,
#(x,y,z) -> (-x,-y,-z)# . It can also be treated as#hatC_2sigma_h# , PROVIDED the#sigma_h# element is perpendicular to the#C_2# axis (and it may not be).
If you have a hard time with this, this website really helps with visualization.
Then, this flow chart may make it easier. However, I don't really use it, so finding point groups can be done without a flow chart except for really complicated molecules.
Here is my thought process for finding the point group of
- It has a single
#C_3(z)# axis perpendicular to its plane (#120^@# rotation), and that is the highest-order rotation axis, so it is the principal rotation axis and we call it the#z# axis by convention. - We see that the
#bb(sigma_h(xy))# perpendicular to the#C_3# axis is trivially present because the molecule is planar (it reflects onto itself and appears to do nothing). - There is a
#bb(C_2"'")# axis perpendicular to the#bb(C_3(z))# , but coplanar with the#sigma_h (xy)# .
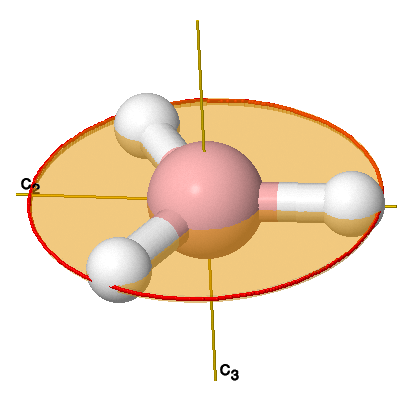
That is enough to conclude that we have a
VIBRATIONAL DEGREES OF FREEDOM
Lastly, the degrees of vibrational freedom for nonlinear polyatomic molecules are found as:
#"DOF"_(vib) = 3N - 6# where
#N# is the number of atoms. (For linear polyatomic molecules, like#"CO"_2# , it would have been#3N - 5# .)
Thus,

