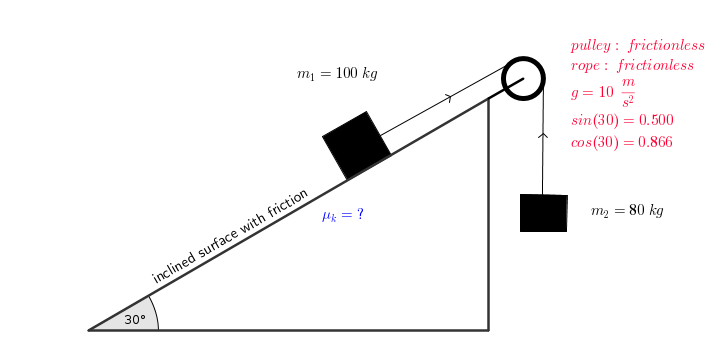
Due to friction ,the system as shown in the diagram remains motionless. Calculate the static coefficient of friction ?
1 Answer
Explanation:
Here's what I tried.
- I defined up the ramp as the positive direction.
Forces on
#sumF_x=T_1-(F_G)_x-f_s=0#
#sumF_y=n-(F_G)_y=0#
-
#f_(s"max")=mu_sn# -
#(F_G)_x=m_1gsin(theta)# -
#(F_G)_y=m_2gcos(theta)# -
#n=mgcos(theta)#
I will refer to
#f_(s"max")# simply as#f_s# from this point on, though I am still solving in terms of the maximum static friction.
Forces on
#sumF=sumF_y=T_2-F_G=0#
#F_G=m_2g#
Because we can assume a massless rope and frictionless pulley,
#T_1=T_2=m_2g#
#=>mu_s=(m_2g-m_1gsin(theta))/(m_1gcos(theta))#
#=>mu_s=(cancel(g)(m_2-m_1sin(theta)))/(cancel(g)(m_1cos(theta))#
#=>color(darkblue)(mu_s=(m_2-m_1sin(theta))/(m_1cos(theta)))#
Using known values:
#mu_s=(80-100(0.500))/(100(0.866))#
#mu_(s"max")=0.346#
#=>mu_s<=0.346#

