To find the diagonal of the cube, there are #2# methods, using a formula or by using the Pythagorus Theorem. So that this explanation is more interesting - and so that you're not just putting numbers into a formula - I am going to tell you how to do the Pythagorus theorem way.
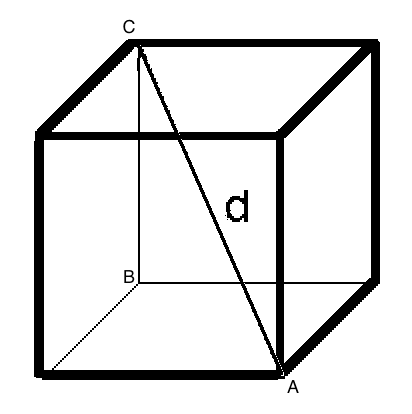
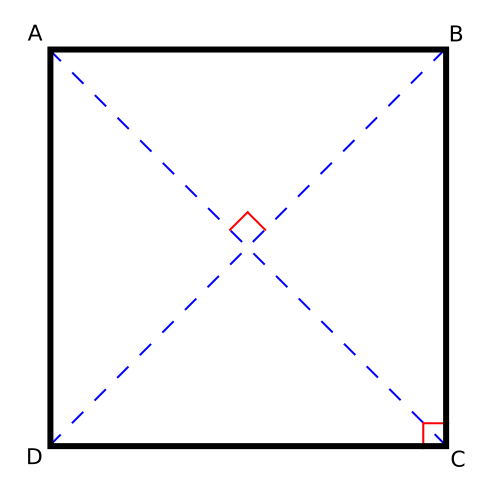
To do this, we need to find the length of the diagonal of the face, in this diagram, from #A# to #B# and then we can construct a triangle with #AB# and #BC# as the two legs, and #CA# as the hypotenuse.
We can find the diagonal by using the Pythagoras Theorem.
First, we need to find the length of #AB#.
#a^2 + b^2 = c^2#
#s^2 + s^2 = d^2#
#s^2 2 = d^2#
#s = 5#
#5^2 2 = d^2#
We can now use algebra to find out the length of the diagonal of the square, which is the shorter diagonal of the cube.
#5^2 2 = d^2#
#25 xx 2 = AB^2#
#50 = AB^2#
#AB^2 = 50#
#AB = sqrt50#
#sqrt50#
#sqrt50 = sqrt2 xx sqrt(5^2#
#sqrt50 = sqrt2 xx 5#
#sqrt50 = 5sqrt2#
#color(lime)(AB = 5sqrt2#
Now we can construct the triangle and find the overall longer diagonal of the cube.
#a^2 + b^2 = c^2#
#AB^2 + BC^2 = CA^2#
#AB = 5sqrt2#
#BC = 5# because #BC# is simply an edge of the cube.
#(5sqrt2)^2 + 5^2 = CA^2#
Now we can use algebra to find #CA#
#sqrt50^2 + 5^2 = CA^2#
The square root and square of #50# cancel each other out.
#50 + 5^2 = CA^2#
#50 + 25 = CA^2#
#75 = CA^2#
#sqrt75 = sqrt(CA^2#
#sqrt75 = CA#
#sqrt75 ~~ 8.660#
#75 = 3 xx 5^2#
#sqrt75 = sqrt3 xx sqrt(5^2#
#sqrt75 = sqrt3 xx 5#
#sqrt75 = 5sqrt3#
#color(blue)(CA = sqrt75#
#color(blue)(CA = 5sqrt3#
#color(blue)(CA ~~8.660#
And if you wanted to do it the other way, the formula is:
#d = sqrt3 xx a#
#d = sqrt3 xx 5#
#color(blue)(d = 5sqrt3#
Hope this helped. :)




