Question

Effective atomic number of `Fe` in `Fe_"2"(CO)_"9"` is ??

Answer 1

It would be `38`. You can find some worked examples here for counting the electrons surrounding the transition metal given by the ligands.

You can also find a worked effective atomic number example here.

---

The effective atomic number corresponds to the total number of electrons around the transition metal given by the ligands, PLUS the total number of electrons the transition metal brings.

Two methods are common to find the electrons donated by the ligands, which I will call:

• the Donor Pair method (Method A)
• the Neutral Ligand method (Method B)

THE DONOR PAIR METHOD

This method considers the ligand to donate a lone pair of electrons, and assigns the charges and atomic oxidation states accordingly. So, `"H"` atom or `"Cl"` atom would be considered as `"H":^(-)` or `"Cl":^(-)`, respectively, either donating two electrons.

THE NEUTRAL LIGAND METHOD

This method considers the ligand to give as many electrons for the bond as it would have if it were neutral. So, `"H"` atom or `"Cl"` atom would be considered as `"H"cdot` or `"Cl"cdot`, respectively, either donating one electron.

The following table lists the number of donated electrons considered using both methods:

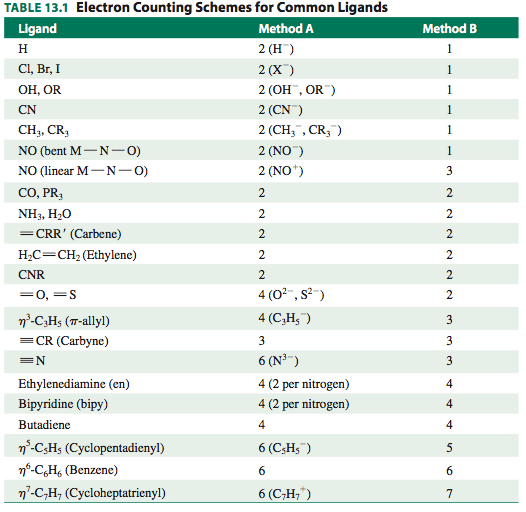
EXAMINING `bb("Fe"_2("CO")_9)`

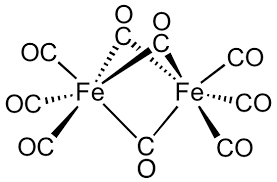
Since this compound is symmetric about the vertical mirror plane perpendicular to the screen (the plane perpendicular to the `"Fe"-"Fe"` axis), we can consider either iron atom and it will be identical to the other. Choose the left one just because.

In the case of `"CO"`, it doesn't matter:

`:"C"-="O":`

It has a lone pair, and it is neutral, so it donates two electrons under either method. The `6 xx "CO"` ligands around a given `"Fe"` atom then ultimately contribute a total of

`6 xx 2 = bb12` electrons

to the effective atomic number.

`"Fe"` in this compound has an oxidation state of `bb0`, because `"CO"` contributes no charge, and both iron atoms must be identical oxidation states by symmetry.

Thus, `"Fe"` in this case will contribute `bb26` electrons to the effective atomic number, as it is neutral and has an atomic number of `26`.

That means its effective atomic number is

`6 xx 2 + 26 = color(blue)bb(38)`