Question

Equal volumes of `"0.25 M"` `"HNO"_2` and `"0.25 M"` `"HNO"_3` are titrated separately with `"0.25 M"` `"KOH"`. Which would be the same for both titrations?

a) initial pH
b) pH halfway to the equivalence point
c) pH at the equivalence point
d) pH when 5 mL excess KOH has been added

I know the answer is D but I don't understand why, could someone explain? Thanks a million ! (:

Answer 1

The answer is indeed (d).

Explanation:

!! LONG ANSWER !!

As you know, you're dealing with nitrous acid, `"HNO"_2`, a weak acid, and nitric acid, `"HNO"_3`, a strong acid.

Right from the start, this tells you that point (a) cannot be true because the weak acid does not dissociate completely in aqueous solution to produce hydronium cations.

This implies that the concentration of hydronium cations will be greater in the solution that contains the strong acid, which, in turn, means that the `"pH"` of the strong acid will be lower than the `"pH"` of the weak acid.

So in terms of initial `"pH"` values, you have

`"pH"_ ("0 HNO"_ 2) > "pH"_ ("0 HNO"_3)`

Now, point (b) cannot be true because, at the half-equivalence point, the `"pH"` of the nitrous acid solution will be equal to the `'p"K_a` of the weak acid.

This is the case because the half-equivalence point, the nitrous acid solution will contain equal concentrations of nitrous acid and nitrite anions, `"NO"_2^(-)`, the conjugate base of nitrous acid, i.e. you are now in the buffer region.

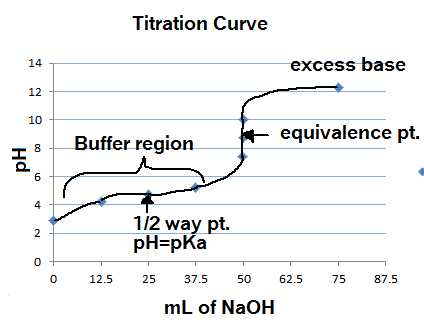
By comparison, at the half-equivalence point, the `"pH"` of the strong acid solution will be lower than the `"pH"` of the weak acid solution because the strong acid is fully dissociated in aqueous solution.

This implies that adding the strong base will only reduce the concentration of the hydronium cations produced by the full ionization of the strong acid.

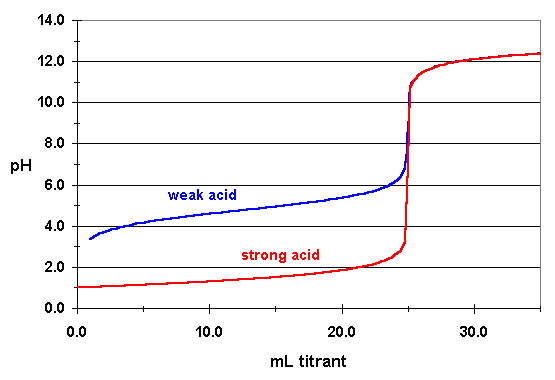
Keep in mind that unlike the nitrite anion, which acts as a weak base, you can assume that the nitrate anion does not act as a base in aqueous solution, i.e. that it will not react with water to reform nitric acid.

Point (c) cannot be true because at the equivalence point, the `"pH"` of the weak acid solution will actually be `>7` while the `"pH"` of the strong acid solution will be equal to `7` at `25^@"C"`.

This is the case because once the neutralization is complete, the weak acid solution will still contain nitrite anions, `"NO"_2^(-)`, which will react with water to produce hydroxide anions and reform some of the nitrous acid.

`"NO"_ (2(aq))^(-) + "H"_ 2"O"_ ((l)) rightleftharpoons "HNO"_ (2(aq)) + "OH"_ ((aq))^(-)`

This will cause the `"pH"` of the solution to be `>7`, i.e. the resulting solution will be basic.

Since the nitrate anion does not react with water to produce hydroxide anions and reform some of the nitric acid, the resulting solution will be neutral and it will have `"pH" = 7`.

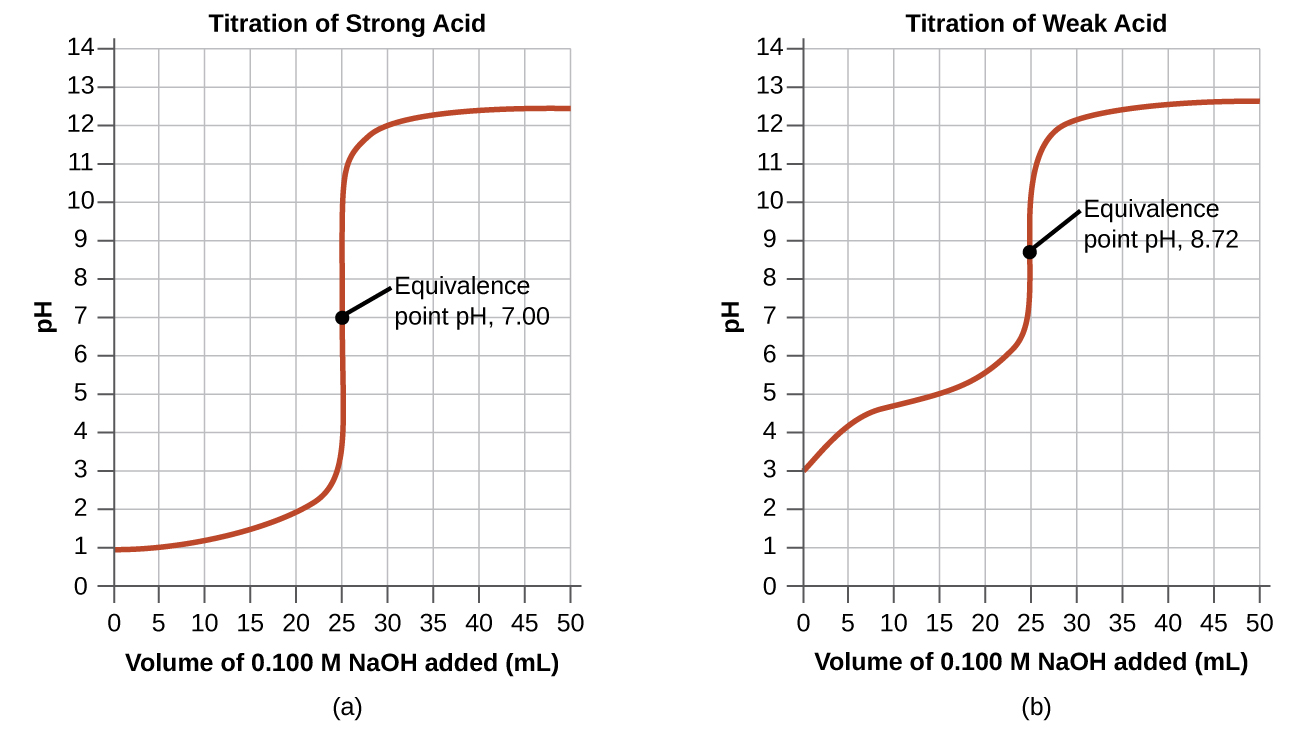
Finally, point (d) is correct because adding `"5 mL"` of excess potassium hydroxide, a strong base, will cause the `"pH"` of the two solutions to reach the same level.

This happens because even though the `"pH"` of the weak acid solution is already `>7` and the equivalence point, the concentration of hydroxide anions it already contains will not be high enough to affect the excess hydroxide anions coming from the strong base.

In other words, for the weak acid solution, you can use the approximation

`["OH"^(-)] = ["OH"^(-)]_ "already present" + ["OH"^(-)]_ "from excess strong base"`

`["OH"^(-)] ~~ ["OH"^(-)]_ "from excees strong base"`

By comparison, once you add the excess strong base, the strong acid solution, which at the equivalence point contains the very small concentration of hydroxide anions produced by the auto-ionization of water

`["OH"^(-)] = 1 * 10^(-7)color(white)(.)"M" ->` a neutral aqueous solution at `25^@"C"`

will have

`["OH"^(-)] = 1 * 10^(-7)color(white)(.)"M" + ["OH"^(-)]_ "from excess strong base"`

`["OH"^(-)] ~~ ["OH"^(-)]_ "from excess strong base"`

This is why the `"pH"` of the two solutions will be equal after `"5 mL"` excess strong base is added. In both cases, you have

`"pH" = 14 - [-log(["OH"^(-)]_ "from excess strong base")]`

hence why point (d) is true.