Evaluate the following?
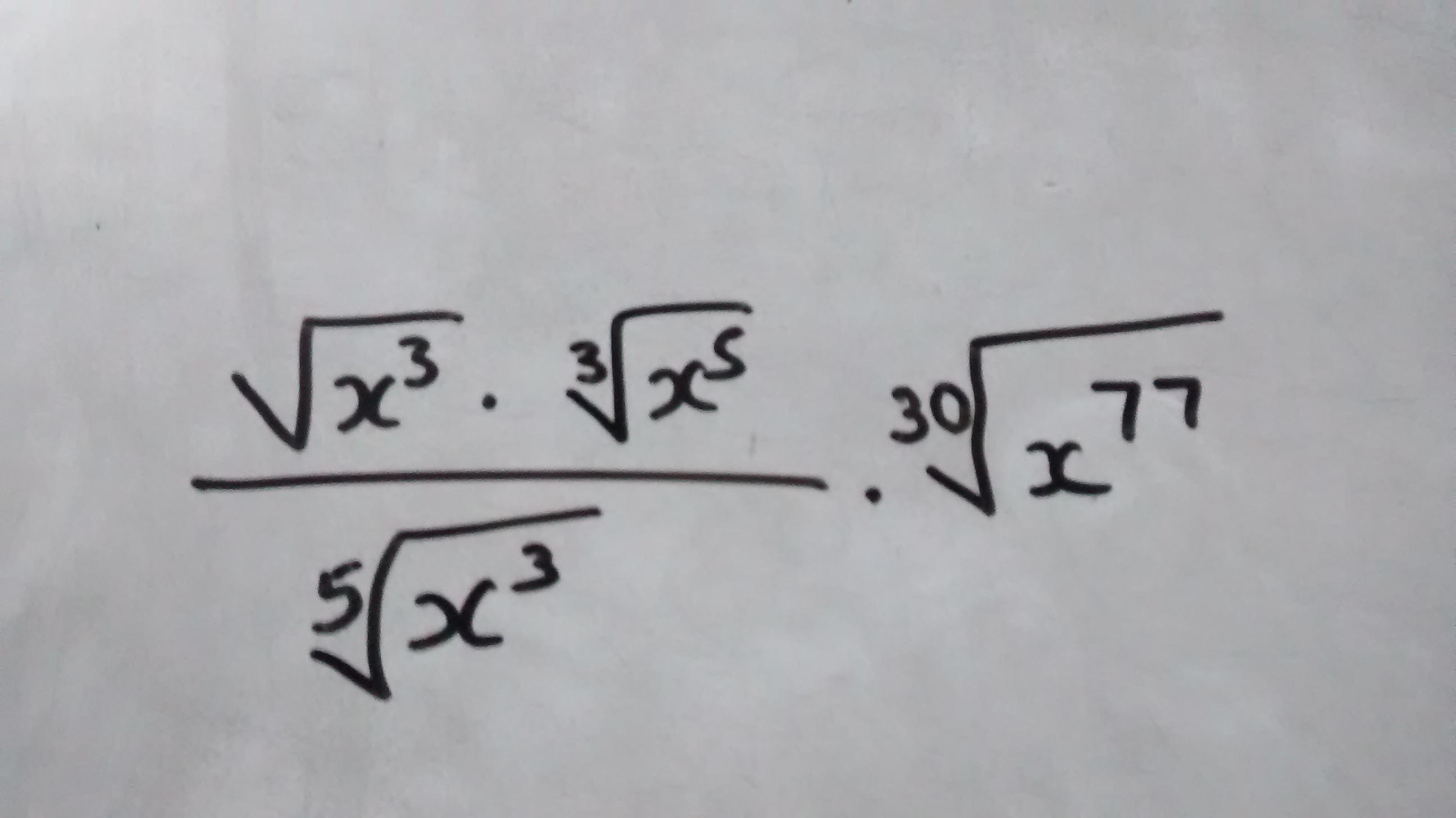
1 Answer
Oct 26, 2016
Explanation:
Using the
color(blue)"laws of exponents"
color(orange)"Reminder " color(red)(bar(ul(|color(white)(2/2)color(black)(a^(m/n)=root(n)(a^m))color(white)(2/2)|))) and
color(red)(bar(ul(|color(white)(2/2)color(black)(a^mxxa^n=a^(m+n) , a^m/a^n=a^(m-n) ,a^-mhArr1/a^m)color(white)(2/2)|))) The above expression can be written as.
x^(3/2)xxx^(5/3)xxx^(77/30)xxx^(-3/5)
=x^(3/2+5/3+77/30-3/5) This now becomes a fraction exercise. That is.
3/2+5/3+77/30-3/5
=45/30+50/30+77/30-18/30=154/30=77/15 Thus our simplification is.
x^(77/15)=root(15)(x^(77)
