Evaluate the following?
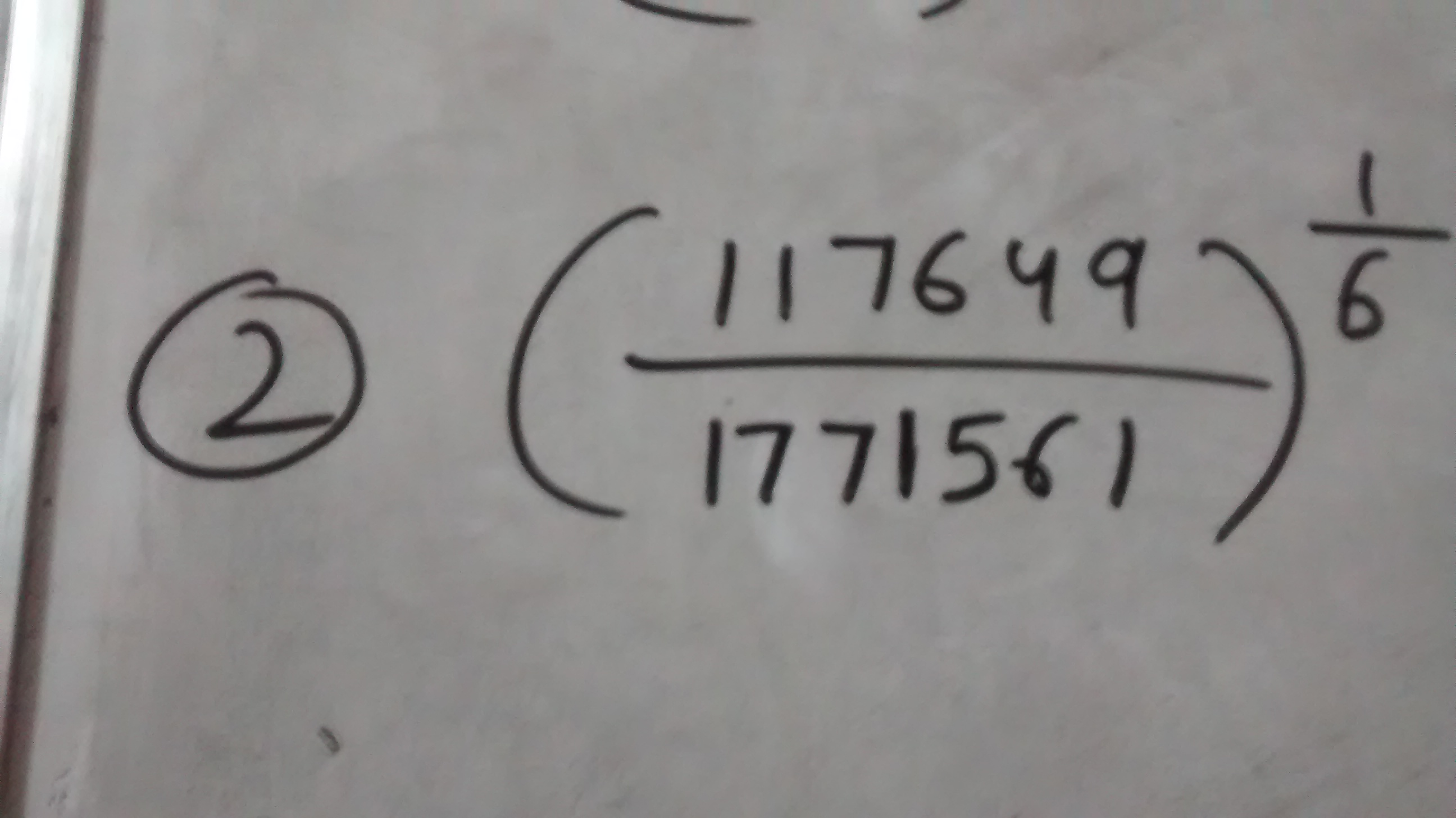
5 Answers
Explanation:
Using the rules of exponents that
=(7^6)^(1/6)/(11^6)^(1/6)
=7^(6*1/6)/11^(6*1/6)
=7^1/11^1
=7/11
Explanation:
This is exactly the same concept as a previous question with an index of
=
Explanation:
Check
- Last digit is odd, so not divisible by
2 . - Sum of digits is
1+1+7+6+4+9 = 28 not divisible by3 . - Last digit is not
0 or5 , so not divisible by5 117649/7 = 16807 , so divisible by7 16807/7 = 2401 2401/7 = 343 343/7 = 49 49/7 = 7
So
So if the answer is exact, we require the denominator to be a perfect
Let's do some approximating...
1771561/117649 ~~ 177/12 ~~ 14
sqrt(14) ~~ 4
root(3)(4) ~~ 3/2
So:
3/2*7 ~~ 11
Try:
1771561/11 = 161051 161051/11 = 14641 14641/11 = 1331 1331/11 = 121 121/11 = 11
So
Hence:
(117649/1771561)^(1/6) = (7^6/11^6)^(1/6) = 7/11
Explanation:
Computing the rational number with fractional exponent
example of:
The rational number above
Prime Factorization :
Then we apply the power of a power with base
Calculator reveals the value as
0.6363636363..





