Evaluate the following?
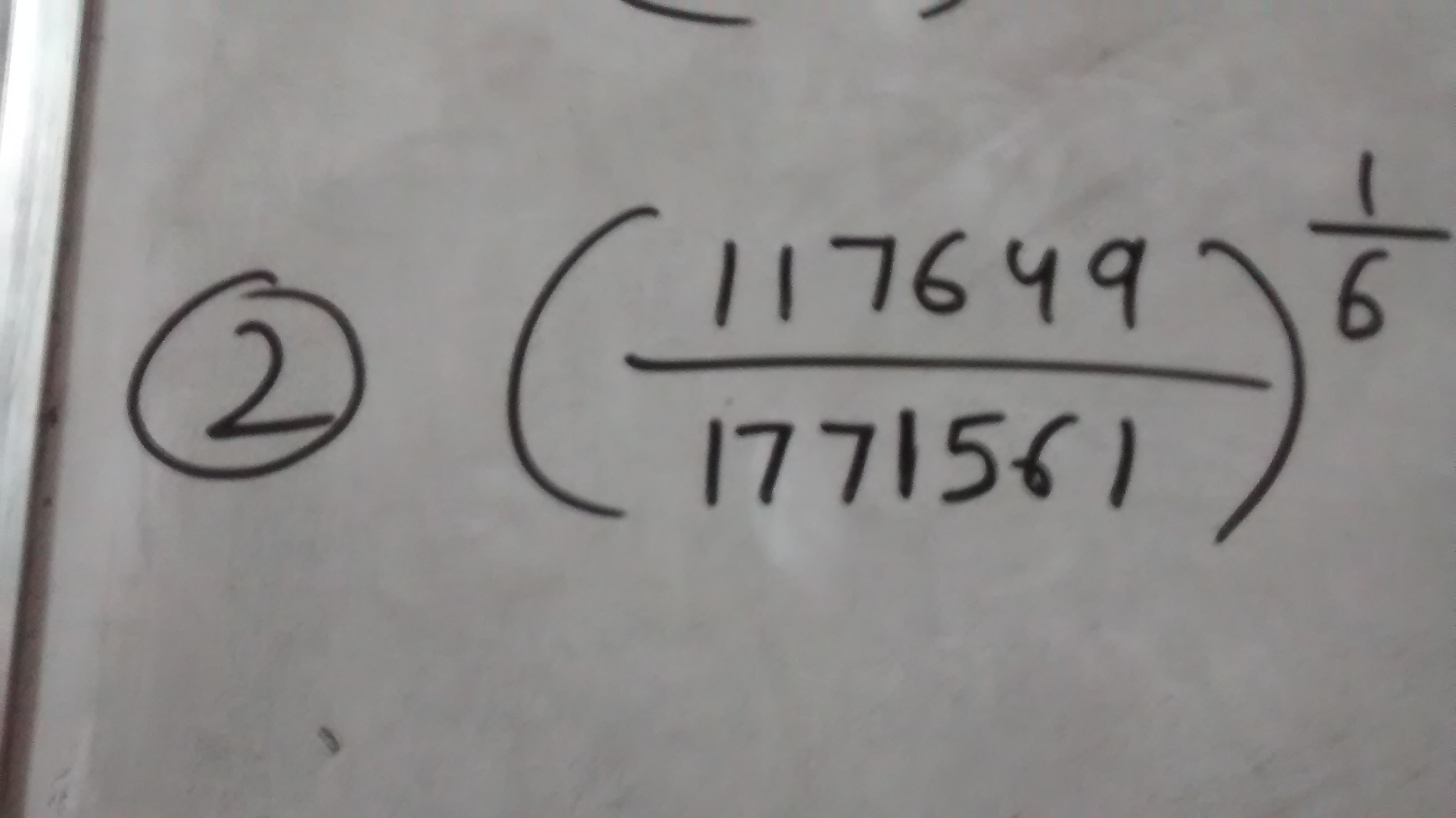
5 Answers
Explanation:
Using the rules of exponents that
#=(7^6)^(1/6)/(11^6)^(1/6)#
#=7^(6*1/6)/11^(6*1/6)#
#=7^1/11^1#
#=7/11#
Explanation:
This is exactly the same concept as a previous question with an index of
=
Explanation:
Check
- Last digit is odd, so not divisible by
#2# . - Sum of digits is
#1+1+7+6+4+9 = 28# not divisible by#3# . - Last digit is not
#0# or#5# , so not divisible by#5# #117649/7 = 16807# , so divisible by#7# #16807/7 = 2401# #2401/7 = 343# #343/7 = 49# #49/7 = 7#
So
So if the answer is exact, we require the denominator to be a perfect
Let's do some approximating...
#1771561/117649 ~~ 177/12 ~~ 14#
#sqrt(14) ~~ 4#
#root(3)(4) ~~ 3/2#
So:
#3/2*7 ~~ 11#
Try:
#1771561/11 = 161051# #161051/11 = 14641# #14641/11 = 1331# #1331/11 = 121# #121/11 = 11#
So
Hence:
#(117649/1771561)^(1/6) = (7^6/11^6)^(1/6) = 7/11#
Explanation:
Computing the rational number with fractional exponent
example of:
The rational number above
Prime Factorization :
Then we apply the power of a power with base
Calculator reveals the value as
0.6363636363..





