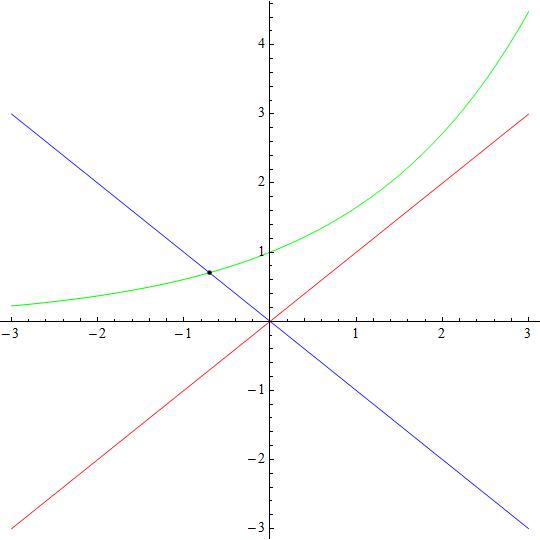
Find the number of real root and the number of imaginary root in the following equation #e^x=x^2# =?
1 Answer
Jul 12, 2016
Explanation:
so
Analyzing the solutions
1)
but
2)
but
Concluding. The solution is
Attached a figure showing:
and the solution point in black