Question

Finding exact area intergration?

Evaluate

`int_-1^4 x(3 − x) dx`.
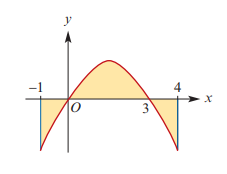
b) Find the exact area of the shaded region in the figure.

Answer 1

`0.83 " sq. units"` (approx.)

Explanation:

We have,

`int_-1^4 x(3 - x)dx`

`= int_-1^4 (3x - x^2)dx`

`= int_-1^4 3x dx - int_-1^4x^2dx`

Let's Evaluate `int_-1^4 3x dx` first.

So,
`= int_-1^4 3x dx = [3/2x^2]_-1^4 = 3/2 4^2 - 3/2 (-1)^2 = 24 - 3/2 = (48 - 3)/2 = 45/2`

And, `int_-1^4x^2dx = [1/3x^3]_-1^4 = 1/3 4^3 - 1/3 (-1)^3 = 64/3 + 1/3 = 65/3`

So, The Actual Integral :-

`int_-1^4 x(3 - x)dx`

`= 45/2 - 65/3 = (135 - 130)/6 = 5/6 = 0.83` (approx)

so, The Area Under the Curve = `0.83 " sq.units"`.

Hope this helps.

Answer 2

The area is `=49/6`

Explanation:

The area is

`int_1^4(3x-x^2)dx=|int_1^0(3x-x^2)dx|+int_0^3(3x-x^2)dx+|int_3^4(3x-x^2)dx|`

`=|[3/2x^2-1/3x^3]_-1^0|+[3/2x^2-1/3x^3]_0^3+|[3/2x^2-1/3x^3]_3^4|`

`=|(0)-(3/2+1/3)|+(27/2-9)+|(24-64/3)-(27/2-9)|`

`=11/6+9/2+11/6`

`=49/6`

Answer 3

The total "actual area" is `49/6`

Explanation:

We seek that "actual" area bounded by the curve `x(3-x)` between `x=-1` and `x=4` as shown in the picture:

We will split this into `3` intervals (actually we could split into `2` and exploit the symmetry of the problem).

First, for convenience, consider the general case:

`I(a,b) = int_a^b \ x(3 − x) \ dx`

`\ \ \ \ \ \ \ \ \ \ = int_a^b \ 3x-x^2 \ dx`

`\ \ \ \ \ \ \ \ \ \ = [3/2x^2-1/3x^3]_a^b \`

`\ \ \ \ \ \ \ \ \ \ = 3/2(b^2-a^2)-1/3(b^3-a^3)`

Then we consider the three regions separately:

`I(-1,0) = 3/2(0-1)-1/3(0+1)`
`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = -3/2-1/3 = -11/6`

`I(0,3) = 3/2(9-0)-1/3(27-0)`
`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = 27/2-9 = 9/2`

`I(3,4) = 3/2(16-9)-1/3(64-27)`
`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = 21/2-37/3 = -11/6` (expected via symmetry)

Then the total "actual area" is:

`A = |I(-1,0)| + |I(0,3)| + |I(3,4)|`
`\ \ \ = |-11/6| + |9/2| + |-11/6|`
`\ \ \ = 11/6 + 9/2 + 11/6`
`\ \ \ = 49/6`

Note this is not the same as the "net" area, where area below the axis is counted negatively, which results in the incorrect answer:

`I(-1,4) = int_(-1)^4 \ x(3 − x) \ dx = 5/6`