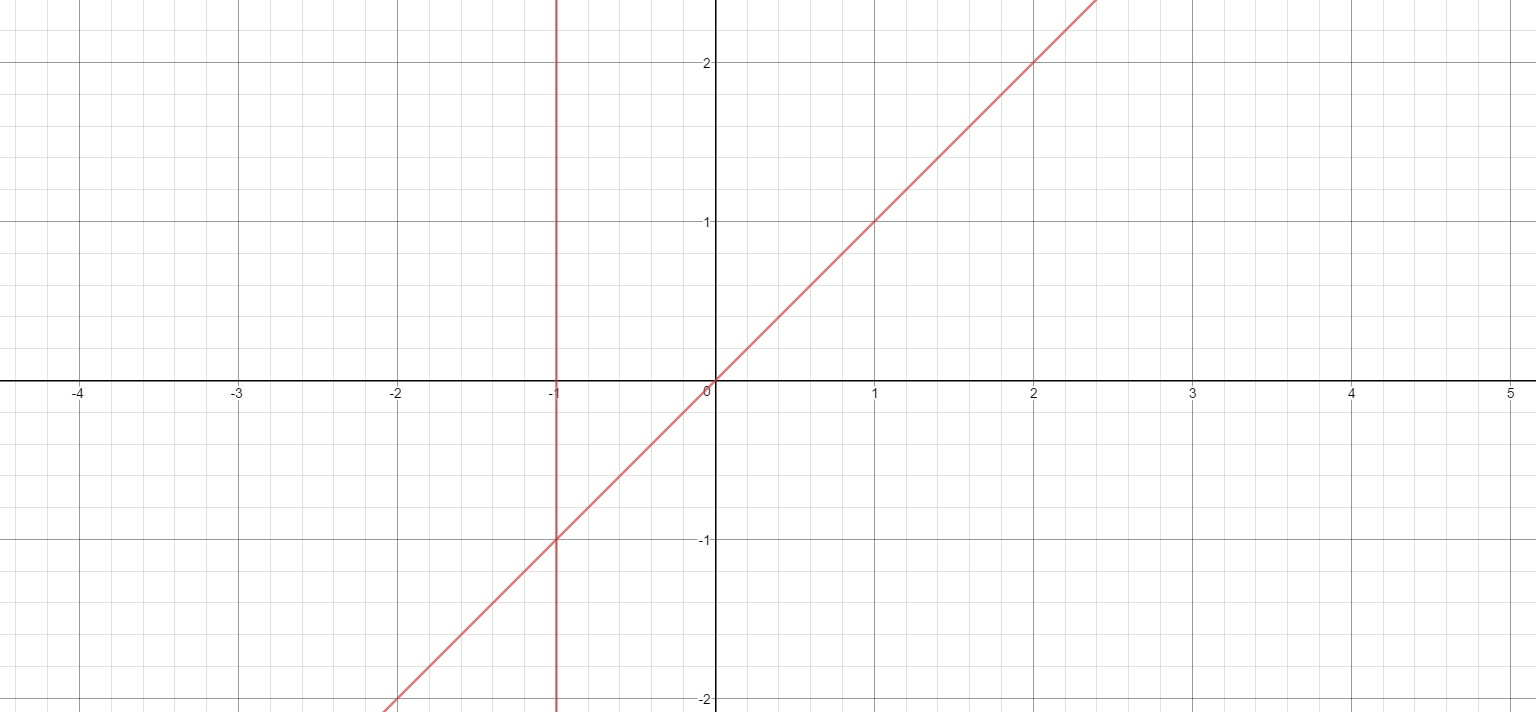
For f(x, y)=x-y, how do you prove that the equation #f(x, y)= x f(y,x)# represents a hyperbola? find its asymptotes?
1 Answer
Oct 22, 2016
The graph is two lines.
Explanation:
Substituting
We'll consider two cases, now:
Case 1:
Then we can divide both sides by
Thus, for
Case 2:
Then
As this is a tautology,
Taken together, our graph becomes two lines: the line with slope