For the circle #(x+3)^2+(y-2)^2=10#, how do you find the equation of the tangent line at the point (-2,5)?
2 Answers
Explanation:
We can evaluate the derivative
In the point
The equation of the tangent line is than:
that is:
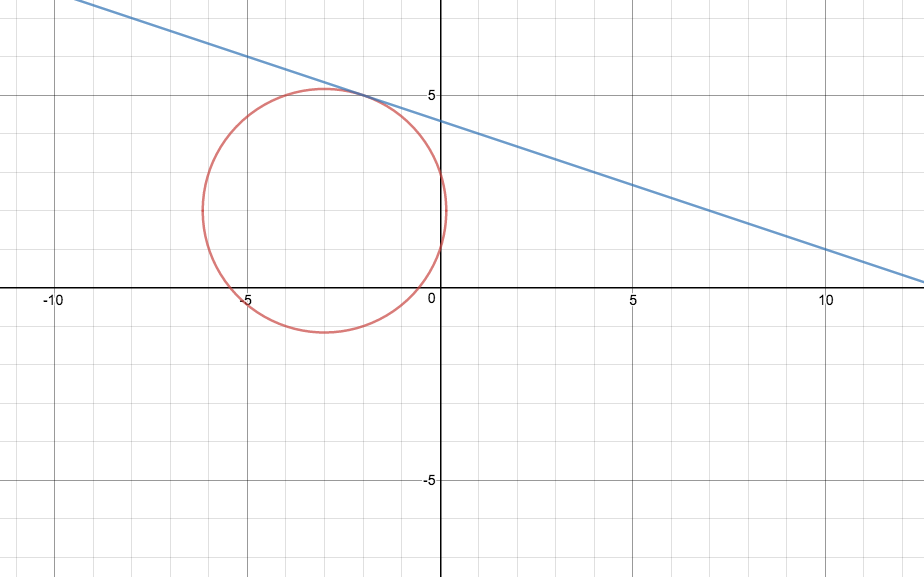
# y = -1/3x+13/3 #
Explanation:
Another approach is using the properties of circles. We have
#(x+3)^2+(y-2)^2=10#
Which represents a circle of centre
First, let us very quickly verify
#(x+3)^2+(y-2)^2=1^2+3^2=10# , which is good!
So the line passing through through
# m_N = (Delta y)/(Delta x) = (5-2)/(-2-(-3)) = 3#
As this perpendicular to the tangent the product of their gradients is
# m_T = -1/3#
So the tangent passes through
# \ \ \ \ \ y-5 = -1/3(x+2) #
# :. y-5 = -1/3x-2/3 #
# :. \ \ \ \ \ \ y = -1/3x+13/3 #


