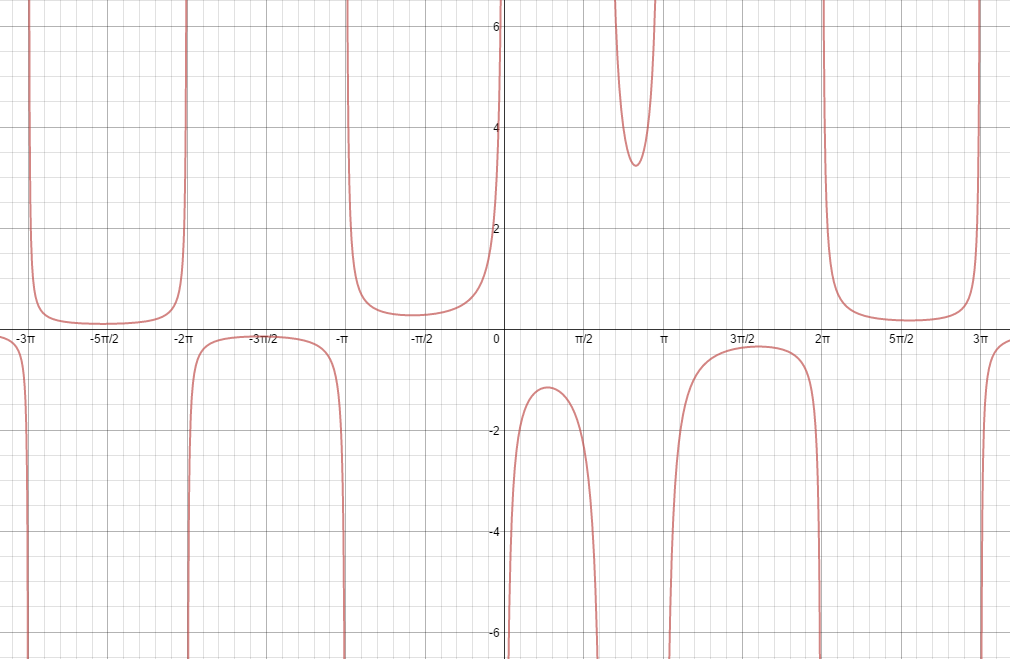
For what values of x, if any, does #f(x) = 1/((x-2)sinx) # have vertical asymptotes?
1 Answer
Mar 13, 2016
Explanation:
Vertical asymptotes occur whenever the denominator equals 0. To find them, we simply set the denominator to 0 and solve, like thus:
We have infinitely many vertical asymptotes, at