Given 2 vectors #A = 4.00i + 3.00j # and #B =5.00i - 2.00 j# how do you find the magnitude & direction of the vector difference A - B?
1 Answer
Jan 24, 2016
We can subtract directly the corresponding components and check using the parallelogram rule.
Explanation:
Have a look:
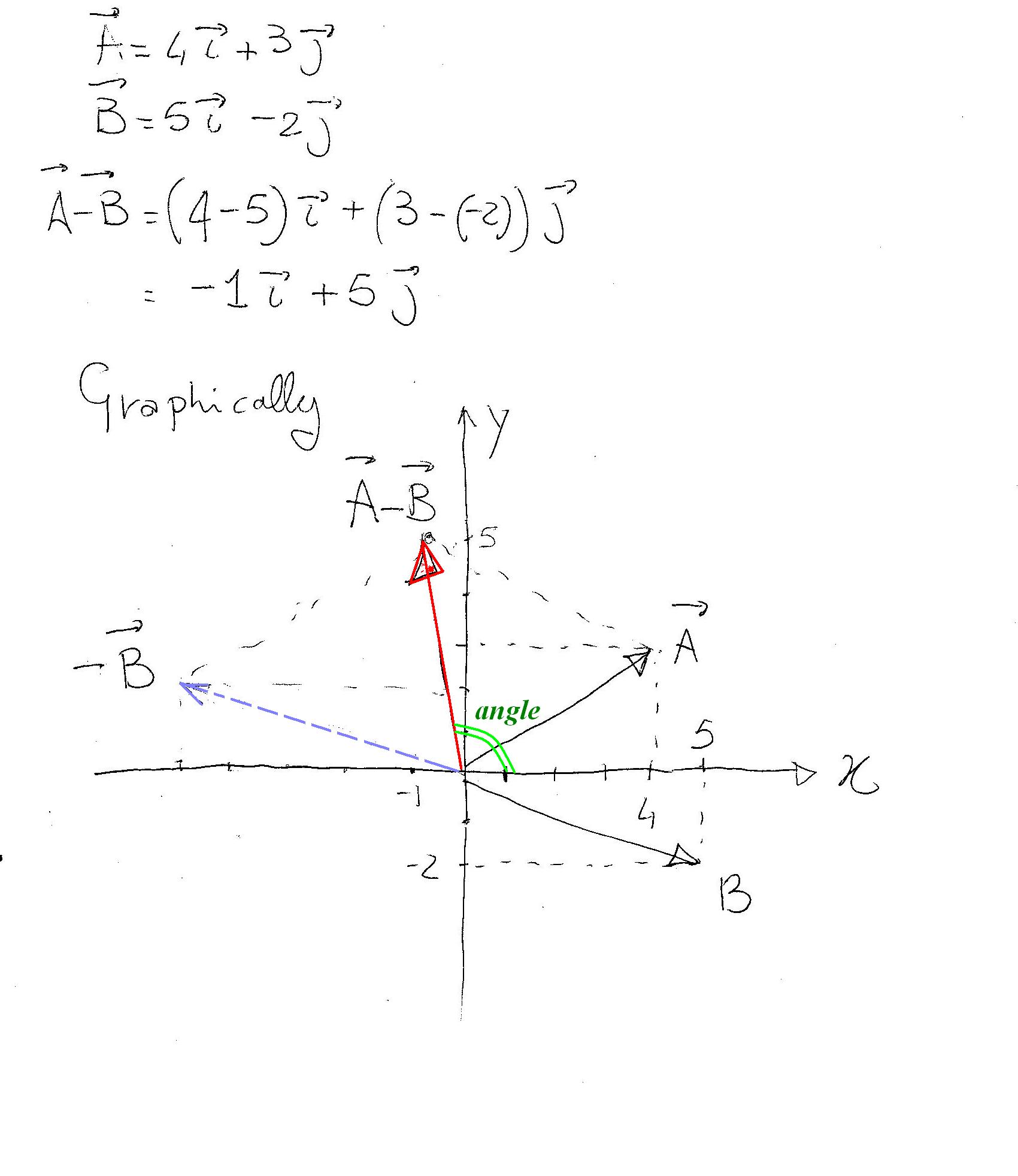
Where, graphically, I used the fact that:
For the magnitude we use Pythagoras (with the components) to get:
For the direction I can see that will be
giving in total: angle

