Given internal coordinates of a molecule (say, #"CCl"_3"Br"#), its relevant bond length(s), and bond angle(s), how do you calculate the moments of inertia in each direction? #r_(C-Br) = "1.91 Å"#, #r_(C-Cl) = "1.77 Å"#, #/_ClCBr = 109.4bar(66)^@#
1 Answer
DISCLAIMER: LONG ANSWER!
Here's the initial setup:
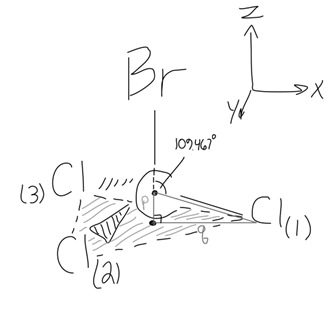
To do this, suppose we already have the initial guess for the internal coordinates in
#""^(79) Br" "" "" "" """^(35)Cl_((1))" "" "" """^(35)Cl_((2))" "" "" """^(35)Cl_((3))#
#"79.919 amu"" ""34.969 amu " ------>#
#x:" "0.0000" "" "1.6688" "" "-0.8344" "" "-0.8344#
#y:" "0.0000" "" "0.0000" "" "" "1.4450" "" "-1.4450#
#z:" "1.9100" "-0.5900" "" "-0.5900" "" "-0.5900#
The idea here is to first find the center of mass coordinates and shift the molecule so that the center of mass lies at
The center of mass coordinates are given by (where
#x_(cm) = (sum_(i) m_i x_i)/(sum_i m_i) = (m_(Br)cdot0 + m_Ccdot0 + m_(Cl)(1.6688 + (-0.8344) + (-0.8344)))/(m_(Br) + m_C + 3m_(Cl))#
#= 0#
#y_(cm) = (sum_(i) m_i y_i)/(sum_i m_i) = (m_(Br)cdot0 + m_Ccdot0 + m_(Cl)(0 + (1.4450) + (-1.4450)))/(m_(Br) + m_C + 3m_(Cl))#
#= 0#
#z_(cm) = (sum_(i) m_i z_i)/(sum_i m_i) = (m_(Br)cdot1.9100 + m_Ccdot0 + m_(Cl)(3*-0.5900))/(m_(Br) + m_C + 3m_(Cl)) = 0.4611#
So, we have the center of mass at
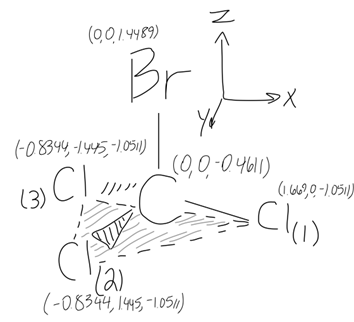
Now that our molecule is set so that the center of mass is at
#I = [(I_(x x),I_(xy),I_(xz)),(I_(xy),I_(yy),I_(yz)),(I_(xz),I_(yz),I_(zz))]# ,where
#I_(pq)# is the component of the inertia tensor that is a function of the#p# and#q# coordinates.
By diagonalizing this matrix, the components of the inertia
This means the tensor looks like this:
#I = [(I_(x x), 0, 0),(0, I_(yy), 0),(0, 0, I_(zz))]#
Instead, all we need to do is sum over all the atoms and evaluate:
#I_(x x) = sum_i m_i(y_i^2 + z_i^2)#
#I_(yy) = sum_i m_i(x_i^2 + z_i^2)#
#I_(zz) = sum_i m_i(x_i^2 + y_i^2)#
We obtain:
#color(blue)(I_(x x)) = overbrace(79.919(0^2 +1.4489^2))^(Br) + overbrace(12(0^2+ 0.4583^2))^(C) + overbrace(34.969(0^2 + 1.0511^2) +2⋅34.969(1.445^2 +1.0511^2))^(Cl_((1)), Cl_((2)), Cl_((3)))#
#=# #color(blue)("432.26 amu" cdot Å^2)#
#color(blue)(I_(yy)) = overbrace(79.919(0^2+1.4489^2))^(Br) + overbrace(12(0^2+0.4583^2))^(C) + overbrace(34.969(1.669^2+1.0511^2) +2⋅34.969(0.8344^2+1.0511^2))^(Cl_((1)), Cl_((2)), Cl_((3)))#
#=# #color(blue)("432.30 amu" cdot Å^2)#
#color(blue)(I_(zz)) = overbrace(79.919(0^2+0^2))^(Br) + overbrace(12(0^2+0^2))^(C) + overbrace(34.969(1.669^2+0^2) + 2⋅34.969(0.8344^2+1.445^2))^(Cl_((1)), Cl_((2)), Cl_((3)))#
#=# #color(blue)("292.13 amu" cdot Å^2)#
For perspective, the evaluated tensor now looks like this:
#I = [(432.26, 0, 0),(0, 432.30, 0),(0, 0, 292.13)]#
The three components of the moment of inertia are given on the diagonal (
#I_(x x) = I_(yy) = "435.603 amu" cdot Å^2#
(#-># #0.76%# error)
#I_(zz) = "293.198 amu" cdot Å^2#
(#-># #0.37%# error)

