Question

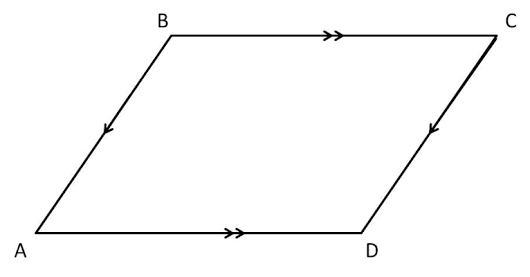
Given Quadrilateral ABCD has coordinates A (3, -5), B (5, -2), C (10, -4), D (8, -7) Quadrilateral ABCD what polygon?

Answer 1

It’s a parallelogram

Explanation:

Given : `A (3,-5), B (5, -2), C (10,-4), D(8,-7)`

Slope `m_(AB) = (-2+5)/(5-3) = 3/2`

Slope `m_(BC) = (-4+2)/(10-5) = -2/5`

Slope `m_(CD) = (-7+4)/(8-10) = 3/2`

Slope `m_(DA) = (-7+5)/(8-3) = -2/5`

Slopes of opposite sides are equal. Hence, they are parallel.

`vec(AB) = srt((5-3)^2 + (-2 + 5)^2) = sqrt13`

`vec(BC) = srt((5-10)^2 + (-2 + 4)^2) = sqrt29`

`vec(CD) = srt((8-10)^2 + (-7 + 4)^2) = sqrt13`

`vec(DA) = srt((8-3)^2 + (-7 + 5)^2) = sqrt29`

Since only opposite sides are parallel and equal, and the product of the slopes of the adjacent sides not equal to (-1), it a simple parallel.