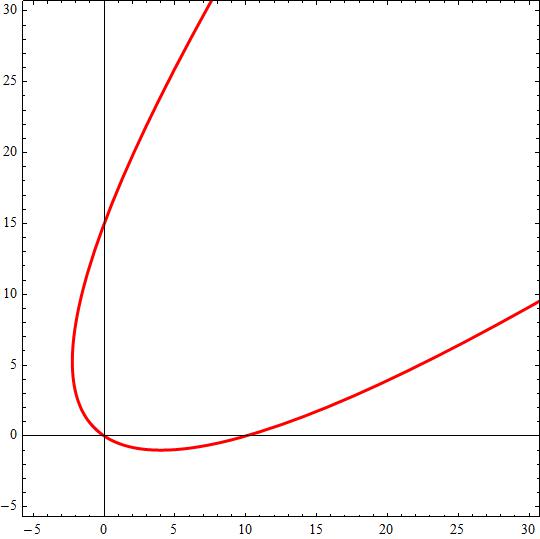
Given that a curve C is represented parametrically by x=t²/2 + 3t y=t²-2t how do you find the value of dy/dx and show that d²2y/dx²=8/(t+3)^3 and Show that C has only one stationary point and that this is a minimum?
1 Answer
Sep 20, 2016
Has a local minimum at
Explanation:
If
them
and
Stationary points are those points that observe
Qualification is done considering the signal of
For
Attached the conic plot.