Question

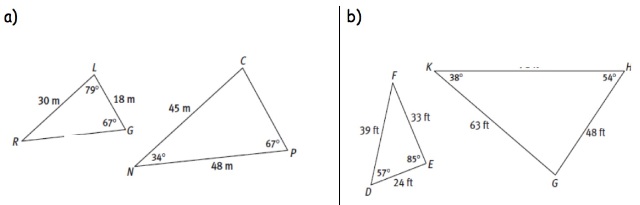
Given the 2 sets of figures below, are the pairs of triangles similar for both set a and set b? Why or why not? What is the similarity statement and the scale factor?

Answer 1

See explanation.

Explanation:

In example `A` triangles are simolar.

The left triangle has angles of: `79`, `67` and `34` degrees.
The last angle can be calculated as: `180-79-67`

The right triangle has angles of `34`, `67` and `79` degrees, so the triangles are similar (angle-angle-angle property)

The scale can be calculated as:

`s=30/45=2/3`

So triangle `RLG` is`2/3` times smaller than `NPC`

In example `B` the triangles are NOT similar.

If they were similar, they would have to have 3 pairs of equal angles. In these triangles there is only one pair of equal angles: `F=K`