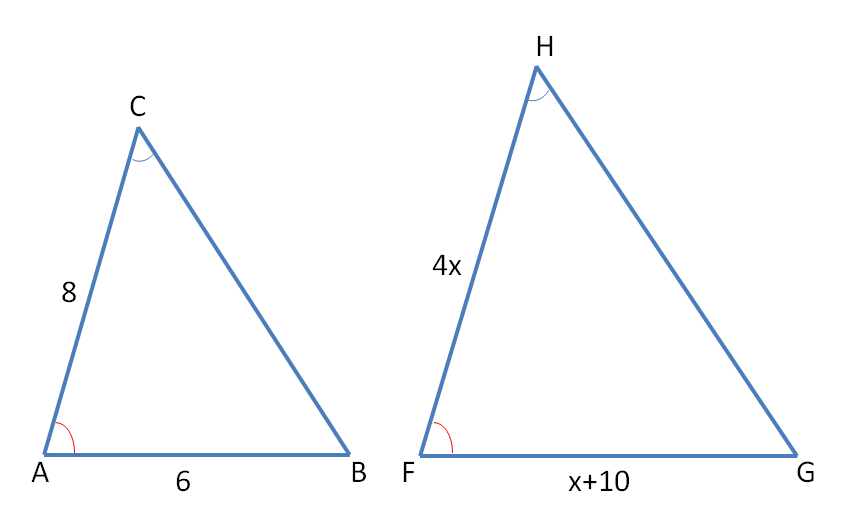
The #DeltasABC# and #FGH# shown below are similar. Find #bar(FH)#?
1 Answer
Mar 14, 2017
Explanation:
As the corresponding angles in
Now as
i.e.
or
or
i.e.
and hence

As the corresponding angles in
Now as
i.e.
or
or
i.e.
and hence