Question

Given the equation N2 + 3F2 --> 2NF3 and the values of deltaH (-264 kJ/mol) and deltaS (-278 J/mol K), what is the standard free energy change for this reaction? B) Use the rxn and table (below) to calculate the average enthalpy of the F-F bond.

bond average bond enthalpy
triple N bond 946
n - f 272
F - F ?

Answer 1

`sf((a))`

`sf(-181color(white)(x)"kJ/mol")`

`sf((b))`

`sf(141color(white)(x)"kJ")`

Explanation:

`sf((a))`

The relationship you need is:

`sf(DeltaG^(@)=DeltaH^(@)-TDeltaS^(@))`

`:.` `sf(DeltaG^(@)=-264xx10^(3)-(298xx-278)color(white)(x)"kJ/mol")`

`sf(DeltaG^(@)=-181color(white)(x)"kJ/mol")`

`sf((b))`

Average bond enthalpies are usually used to estimate the enthalpy change of a reaction.

In this case we are asked to use the enthalpy change to estimate a bond enthalpy.

Energy needs to be put in to break bonds. Energy is released when new bonds are formed. We can say:

`sf(DeltaH)` = energy put in - energy released.

It helps to draw out the structures involved:

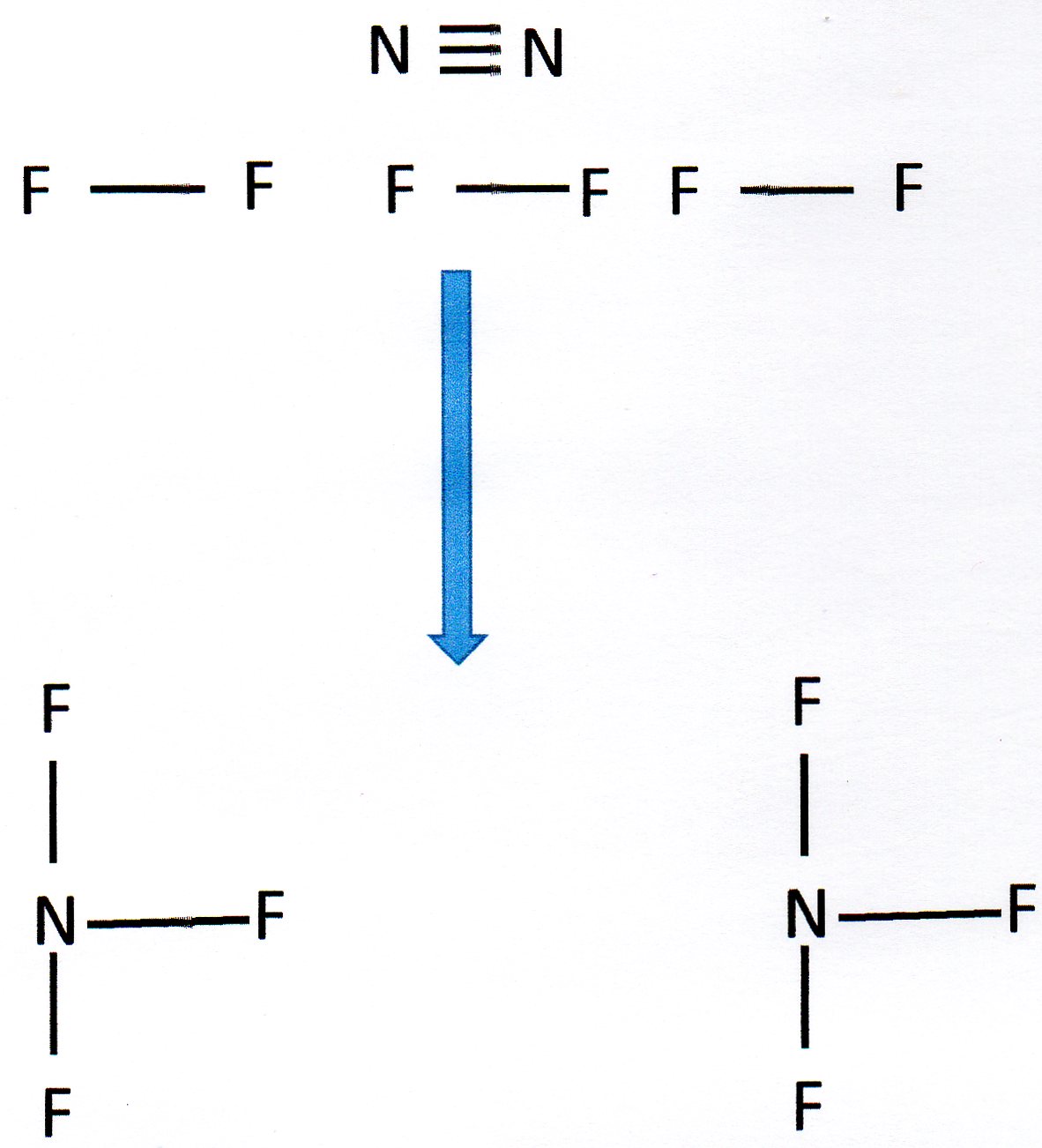
You can see that we need to break 1 N`-=`N bond and 3 F - F bonds.

We then form 6 N - F bonds.

Energy put in = `sf(946+3E(F-F)color(white)(x)kJ)`

Energy released = `sf(6xx272=1632color(white)(x)kJ)`

`sf(DeltaH)` = energy put in - energy released.

`:.` `sf(-264=946+3E(F-F)-1632)`

`sf(3E(F-F)=424color(white)(x)kJ)`

`:.` `sf(E(F-F)=424/3=141color(white)(x)kJ)`