Given the following information, should we expect to be able to assign the C-O bonds to individual peaks, and if so, which mode is associated with which band? Why?
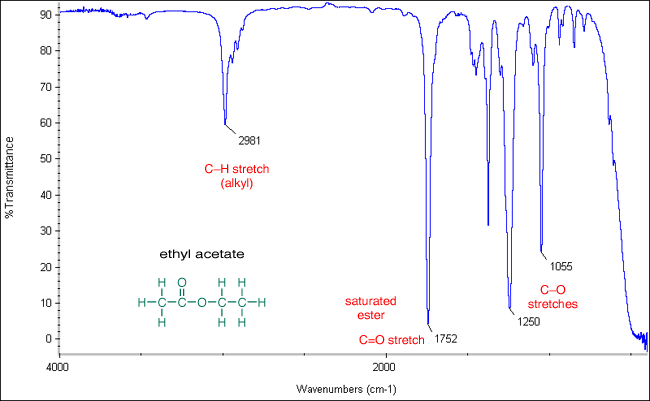
In the IR spectra of acetates, two intense bands are usually observed in the 1270-1000 wavenumber region. These peaks are related to the stretching vibrations of the two C-O bonds of the ester group.
In the IR spectra of acetates, two intense bands are usually observed in the 1270-1000 wavenumber region. These peaks are related to the stretching vibrations of the two C-O bonds of the ester group.
1 Answer
When examining an organic acetate's stretching bands for the
Here are the overall steps we will follow:
- Determine the point group by identifying the symmetry elements of the
#"O"-"C"# carbons. - Determine the reducible representation that corresponds to the carbon
#2s# "group orbitals". - Reduce it to the IRREPs that each correspond to an IR vibrational mode.
- Determine which IRREP corresponds to which mode and from the way the IRREP describes the group orbital behavior, figure out which peak the mode corresponds to.
This can be difficult, so if you have questions, feel free to ask.
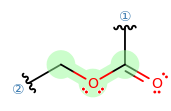
IDENTIFICATION OF THE POINT GROUP SYMMETRY
The first thing I would do is try to identify what point group this belongs to, and then reading its character table can tell us a lot about the IR bands.
There is no principal axis where a rotation around some angle
IMPORTANT: I am using the convention that this is in the
We would draw this out like so:
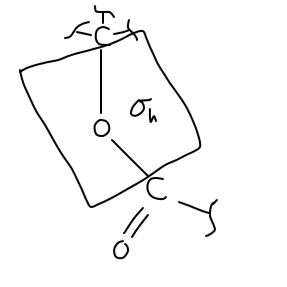
We also, for the sake of completeness, have an identity element
We don't actually have a
Consider this flowchart:
- The molecule is not linear.
- The molecule has no
#C_n# axis with#n > 2# . - It has no
#C_n# axis where#n = 2# . - It has a horizontal mirror plane coplanar with the molecular fragment.
Therefore, it is
UTILIZING THE SYMMETRY OPERATIONS TO DETERMINE THE REDUCIBLE REPRESENTATION
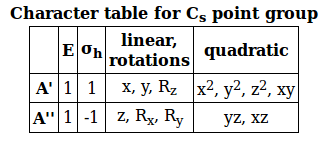
The character table for the
Now, here's the difficult part. What we have to do is determine a reducible representation
Then we can reduce it down to the irreducible representation, or IRREP (such as
- First, we operate with
#hatE# to return the same molecule back. Neither#"O"-"C"# moved, so each contributes#1# to the reducible representation no matter what, for a total of#2# . - Then, we operate with
#sigma_h# to return#1# if we are using the#2s# orbital as a basis, or#-1# if we are using the#2p_z# orbital as a basis, because it merely reflects the molecular fragment through its own plane. We get a total of#2# or#-2# , respectively.
This determination of the reducible representation is something that I sometimes have trouble with, so if you aren't following, definitely ask more about this.
Our reducible representation, using a
#color(green)(Gamma_(2s " AOs") = "2 2")#
REDUCING THE REDUCIBLE REPRESENTATION GIVES THE IRREPS THAT CORRESPOND TO EACH VIBRATIONAL MODE
The equation for reducing this into the IRREPs is:
#\mathbf(1/h sum_("IRREPs") c(hatR)*chi(Gamma)chi(hatR))# where:
#h# is the order, found by summing the coefficients on each operator (all#1# 's). You should get#2# .#c(hatR)# is each coefficient next to the operator#hatX# , which again, is all#1# 's.#chi(Gamma)# is each number in#Gamma# that we just got.#chi(hatR)# is the number along the particular row of the character table that we are looking at.
For the
#Gamma_(A') = 1/2[1*2*1 + 1*2*1] = color(blue)(2)#
#Gamma_(A'') = 1/2[1*2*1 + -1*2*1] = color(red)(0)#
Hence, our IRREP is
Notice the "linear, rotations" column in the character table. In that column, you can find which types of linear motions (linear stretches along which axes) are IR active.
It shows
HOW DOES EACH VIBRATIONAL MODE LOOK?
Alright, now we know:
#A' (y)# is the "totally symmetric" stretch, so it would be when both#"C"-"O"# bonds stretch in and out in the same direction at the same time (in the plane of the molecule).#A' (x)# is the not totally symmetric stretch, so it would be when both#"C"-"O"# bonds stretch in and out at the same time, but one stretches in while the other stretches out (in the plane of the molecule).
If you draw out the "group orbital", which is the joined set of
Each eventually cancels a vector direction to give a net dipole change in one axis (that is shown approximately, in dashed arrows).
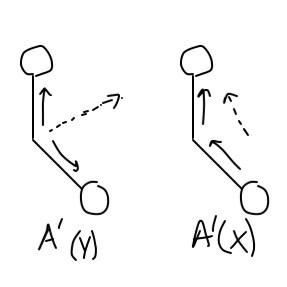
Both are two similar
So indeed, there are TWO IR-active stretches! We can see them here:
NOW HOW DO WE KNOW WHICH ONE IS WHICH?
We're almost there!
- The left bond is an
#sp^3# #"C"-"O"# bond. - The right bond is a relatively
#sp^2# #"C"-"O"# bond.
Therefore, the
The
Since the
If we suppose we have a
So, what I would predict we have is:
#A'(y)# mode:#~"1055 cm"^(-1)#
#A'(x)# mode:#~"1250 cm"^(-1)#
Ask your professor to confirm. :)

