Infrared Spectroscopy
Key Questions
-
Vibrating bonds absorb infrared energy at a frequency that corresponds to the vibrational frequency of the bond.
In organic chemistry, this corresponds to frequencies of 15 to 120 THz.
These frequencies are expressed as wavenumbers:
#"wavenumber" = "frequency"/"speed of light" = ν/c# So the wavenumbers range from 500 to 4000 cm⁻¹.
Molecules do not have rigid bond lengths and bond angles.
Rather, bond lengths and angles represent the average positions about which atoms vibrate.
Each vibration may cause a change in the dipole moment of the molecule. The alternating electrical field of the infrared radiation can interact with the alternating dipole moment.
If the frequency of the radiation matches the vibrational frequency, the bond will absorb the radiation. The amplitude of the vibration will increase.
The spectrometer detects this absorption and records it as a peak in a plot of transmission versus frequency.
Within a narrow range, each type of bond vibrates at a characteristic wavenumber. This makes infrared spectroscopy useful to identify functional groups in a molecule.
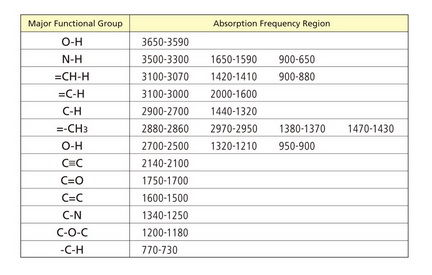
Here’s a short table of common absorption frequencies.

Notice how you can identify the important vibrations in the spectrum of ethyl acetate. The C=O and C-O absorptions tell you that this is an ester.

Here’s a video that gives a simple explanation of infrared spectroscopy.
-
Answer:
The infrared spectrum tells us what functional groups are present in a molecule.
Explanation:
The bonds in molecules are vibrating, and the vibrational energy is quantized.
The bonds can stretch and bend only at certain allowed frequencies.
A molecule will absorb energy from radiation that has the same energy as its vibrational modes.
This energy is in the infrared region of the electromagnetic spectrum.
Each functional group has vibrational frequencies in a small region of the IR spectrum, so IR spectra give us information about the functional groups that are present.
Here is a table that lists the characteristic vibrational frequencies of some functional groups.
-
I like to think of it measuring the shadow of a molecule.
Certain bonds in a molecule vibrate at certain rates/conformations when irradiated by infrared radiation. It is mainly used coupled with nuclear magnetic resonance or mass spectrometry to identify unknown compounds in analytical organic or inorganic chemistry.