Question

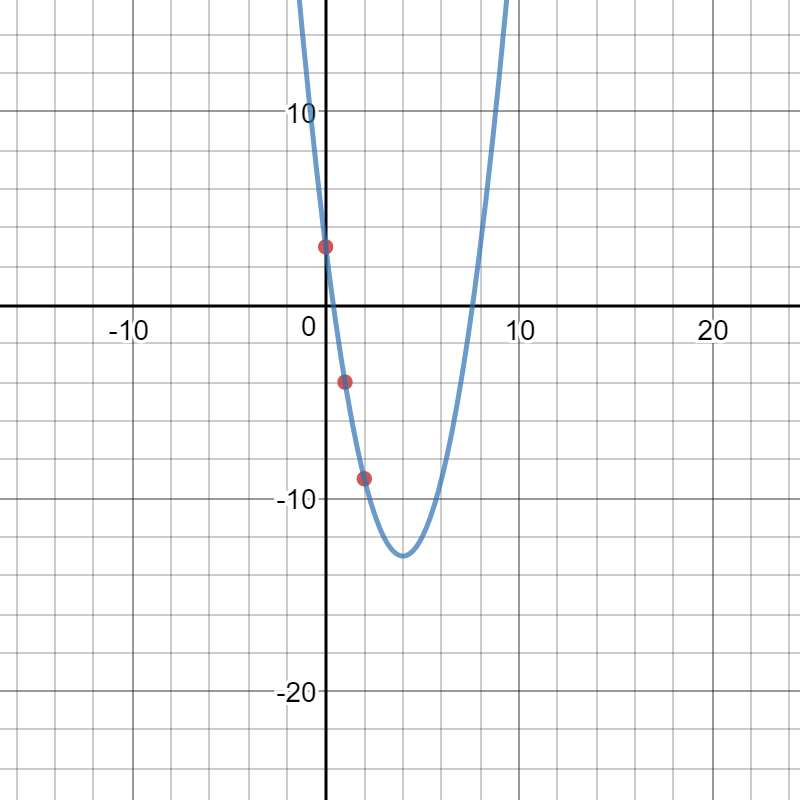
Given three points (0,3),(1,-4),(2,-9) how do you write a quadratic function in standard form with the points?

Answer 1

Use the standard form `y = ax^2+bx+c` and the 3 points to write 3 equations with, a, b, and c as the variables and then solve for the variables.

Explanation:

Because the question specifies a function, we must discard the form that is not a function:

`x = ay^2+by+c`

and use only the form:

`y = ax^2+bx+c" [1]"`

Using the point `(0,3)`, we substitute 0 for x and 3 for y into equation [1] and the solve for c:

`3 = a(0)^2+b(0)+c`

`c=3`

Substitute 3 for c into equation [1]:

`y = ax^2+bx+3" [1.1]"`

Using the point `(1,-4)` we substitute 1 for x and -4 for y into equation [1.1] to obtain an equation that contains "a" and "b" as variables:

`-4 = a(1)^2+b(1)+3`

`a + b = -7" [2]"`

We do the same thing using the point `(2,-9)`

`-9 = a(2)^2+b(2)+3`

`4a+2b = -12" [3]"`

Write equations [2] and [3] together as a system of equations:

`a + b = -7" [2]"`
`4a+2b = -12" [3]"`

Multiply both sides of equation [2] by -2 and add the results to equation [3]:

`4a-2a +2b-2b = -12+14`

This makes the terms containing "b" become 0:

`2a = 2`

`a = 1`

Substitute 1 for "a" into equation [2] and then solve for "b":

`1 + b = -7`

`b = -8`

Substitute 1 for "a" and -8 for "b" into equation [1.1]:

`y = x^2-8x+3" [1.2]"`

Here is a graph of the 3 points and equation [1.2]: