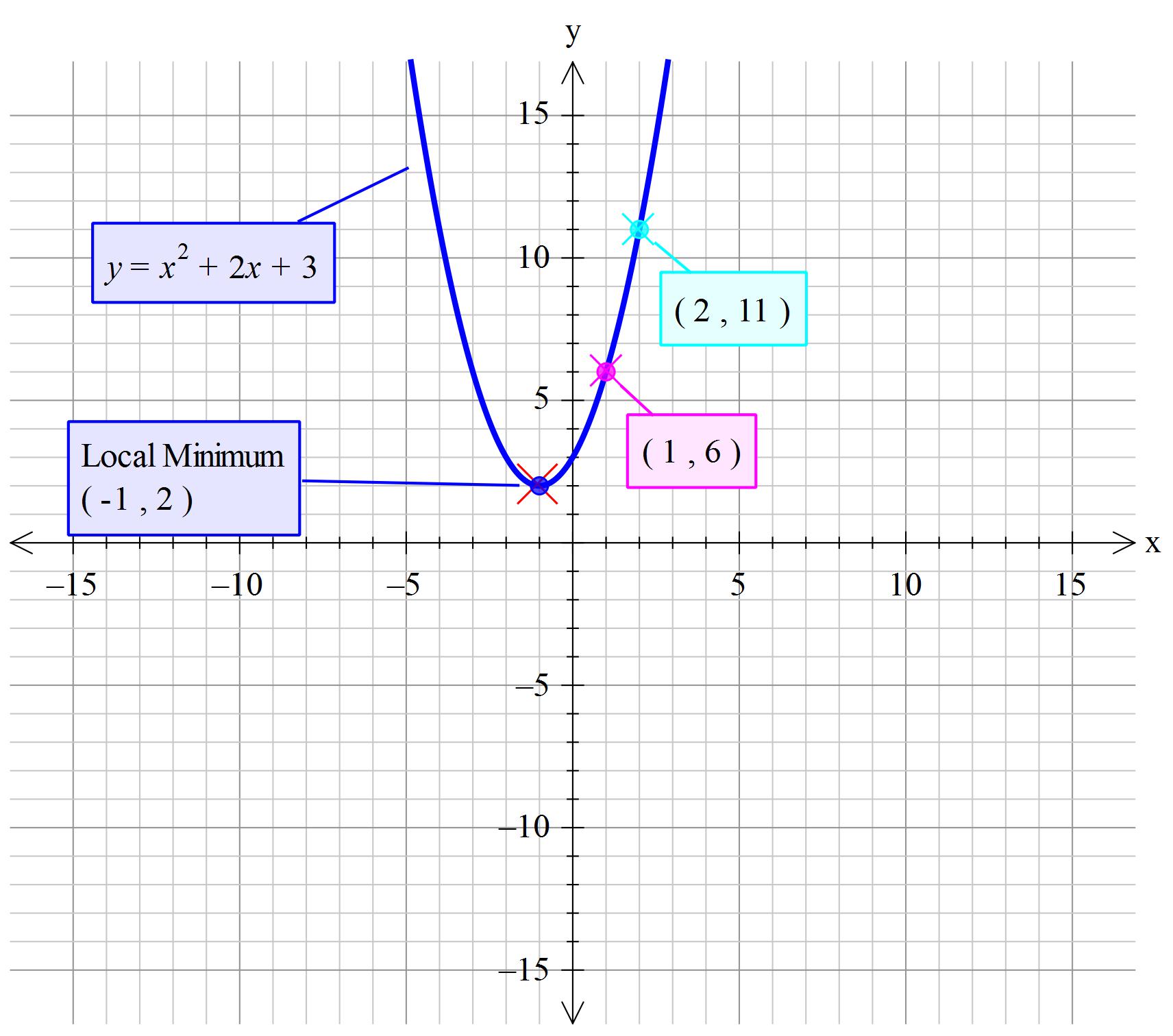
Using standard form of #y=ax^2+bx+c#
For point 1
#P_1->(-1,2) => 2=a(-1^2)+b(-1)+c# .....Equation (1)
For point 2
#P_2->(1,6) => 6=a(1^2)+b(1)+c# .....Equation (2)
For point 3
#P_3->(2,11) => 11=a(2^2)+b(2)+c# .....Equation (3)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Eqn(1)+Eqn(2)
#2=a-b+c larr" Equation (1)"#
#ul(6=a+b+c) larr" Equation (2)"#
#8=2a+0+2c#
Divide both sides by 2
#=>a+c=4# ....................................Eqn(4)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Substitute for #a# and #c# in Eqn(2) using Eqn(4)
#color(brown)(6=a+b+c)color(blue)(->6=4+b)#
#" "color(green)(b=2)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Subtracting #b=2# from both sides of all 3 equations we have
#4=a+c" "............................"Eqn (1_a)#
#4=a+c" "............................"Eqn(2_a)#
#7=4a+c" "........................."Eqn(3_a)#
#Eqn(3_a)-Eqn(2)#
#7=4a+c#
#ul(4=color(white)(.)a+c) larr" Subtract"#
#3=3a+0#
#" "color(green)(=>a=1)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Substitute #a=1# into #Eqn(1_a)#
#4=1+c#
#" "color(green)(=>c=3)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(magenta)("The equation is: "y=x^2+2x+3#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~