H2S (g) concentrations of 660ppm is dangerous. (6) H2S generators continually release all of the gas they can every 15 minutes & the gas is never vented out of a room (vol 198,200L). How long will it take the H2S (g) concentration 2 reach dangerous level?
1 Answer
I don't know if the text of the question is complete, since no mention of how much gas one generator produces in 15 minutes. I'll show everything you have to do to solve this problem up until that point.
So, you know that the threshold for hydrogen sulfide (
For gaseous mixtures like you have here, ppmv, or parts-per-million by volume, is used instead of ppm
Now, I assume that you must use ppm, since ppmv would require additional information, so the fastest way of doing so is by using the density of air, which is approximately
Since I want to keep the calculation simple, I'll assume that the air has a density of
In this case, a concentration of 660 ppm would mean that the room must contain
The volume of the room is
As a result, the mass of hydrogen sulfide will be
I assume that you have six
Let's say every generator produces
SIDE NOTE. The generator is actually called a Kipp generator, also known as KIpp's apparatus
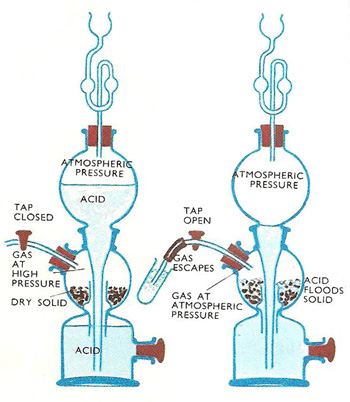
The apparatus uses the reaction between ferrous sulfide and a strong acid (usually hydrochloric acid) to produce hydrogen sulfide gas

