Help! Rotate the axis to eliminate the xy-term in the equation then write the equation ins standard form. x^2-4xy+4y^2+5sqrt(5)+1=0 Help!?
3 Answers
Please see below.
Explanation:
The equation given here
What a rotation does is it changes
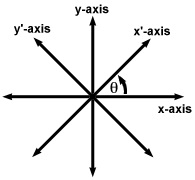
In such a case, the relation between coordinate
and reverse is
Note that latter equations are equivalent to rotation by
In such cases, we can eliminate
In given equation we have
or
These two angles relate to
Hence, either
or
and we have
and putting these in given equation and simplifying we get
One can also try for
i.e
and simplifying
Note - Please observe that above equation
See below.
Explanation:
This possible conic can be written as
Making a coordinate change such that
Choosing
Now substituting this value into the rotation we have
This final result shows that
Please check the original equation. I think there is something wrong.
Explanation:
Here is a reference on Rotation of Axes
The general form of a conic is:
For the given equation:
The angle of rotation is:
Using equations from the reference:
I think there is something wrong;
When I try to graph either the original equation or the rotated equation, using Desmos.com, I get nothing.

