How can spectroscopy be used to identify a gas?
1 Answer
An example is, of course, IR Spectroscopy (since apparently it's the category).
Not many people use IR spectroscopy for gases in undergrad education, but if you have a gas cell, such as this one
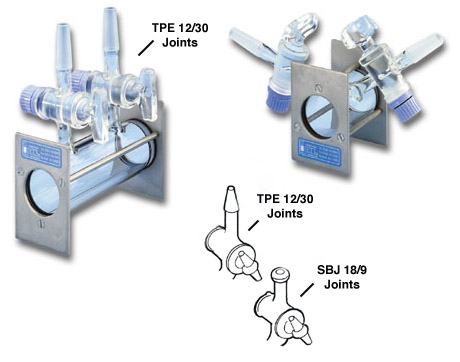
then what you can do is open both valves, let a gas in from a gas tank via a tube, then close both valves as soon as possible after about 5~10 seconds (if you only open one valve, the gas will come in and go right back out).
Then, you can insert it into an IR spectrometer, like a Thermo-Scientific Nicolet iS5 FTIR, for example (FTIRs are used often these days because of their scan rate, high resolution, low noise, etc).
If the signal is too strong, presumably you would have a dilution chamber of sorts, where you can pump the gas into a tube, let it flow to a disposal area, and overall lower the partial pressure of the gas in the gas cell. Then just measure it again and again until the signal is on-scale (below the absorbance point where the graph cuts off).
After you get a proper signal, you would have to identify the ro-vibrational IR spectrum of the gas. For example, an HCl ro-vibrational spectrum looks like this:
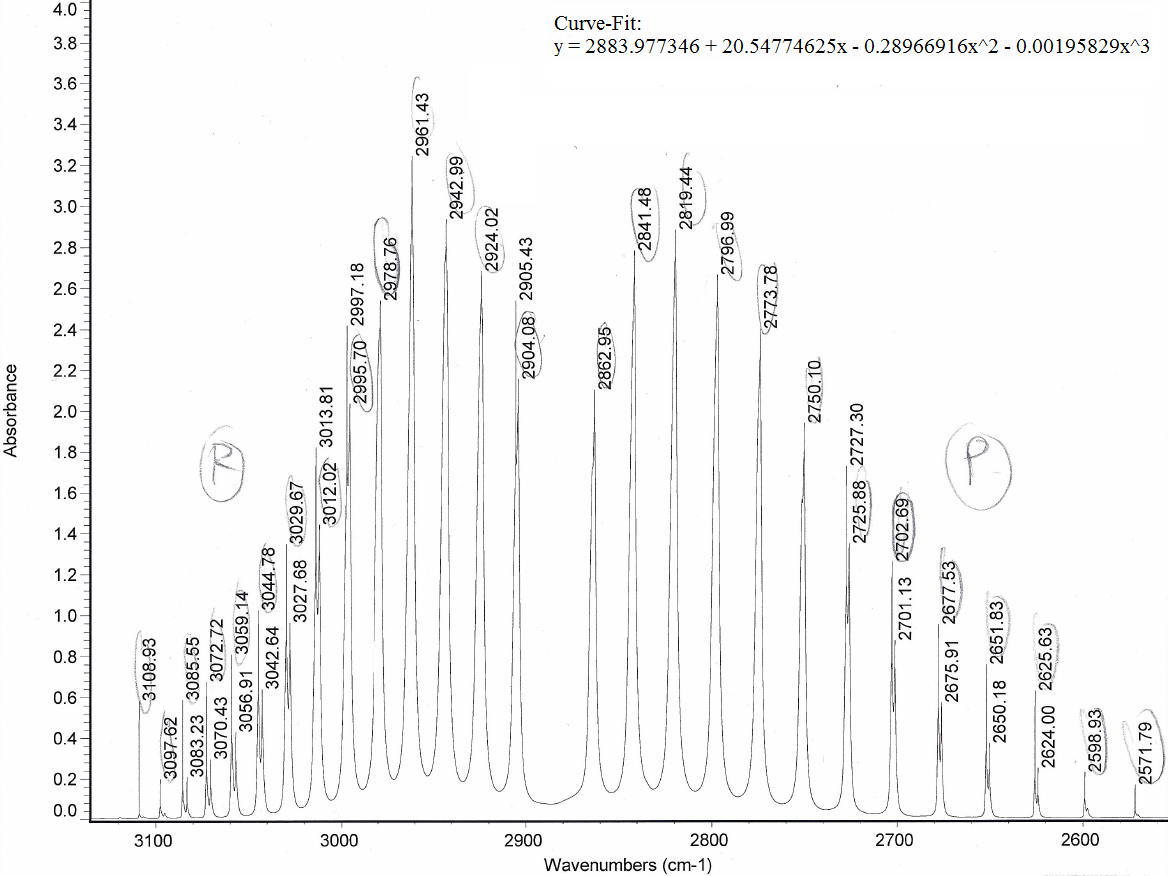 HCl Allowed Transitions The ro-vibrational IR spectrum of HCl in a viewable range for the allowed transitions. The ones visible here are P(1) through P(13) and R(0) through R(13), and the taller peaks were circled.
HCl Allowed Transitions The ro-vibrational IR spectrum of HCl in a viewable range for the allowed transitions. The ones visible here are P(1) through P(13) and R(0) through R(13), and the taller peaks were circled.
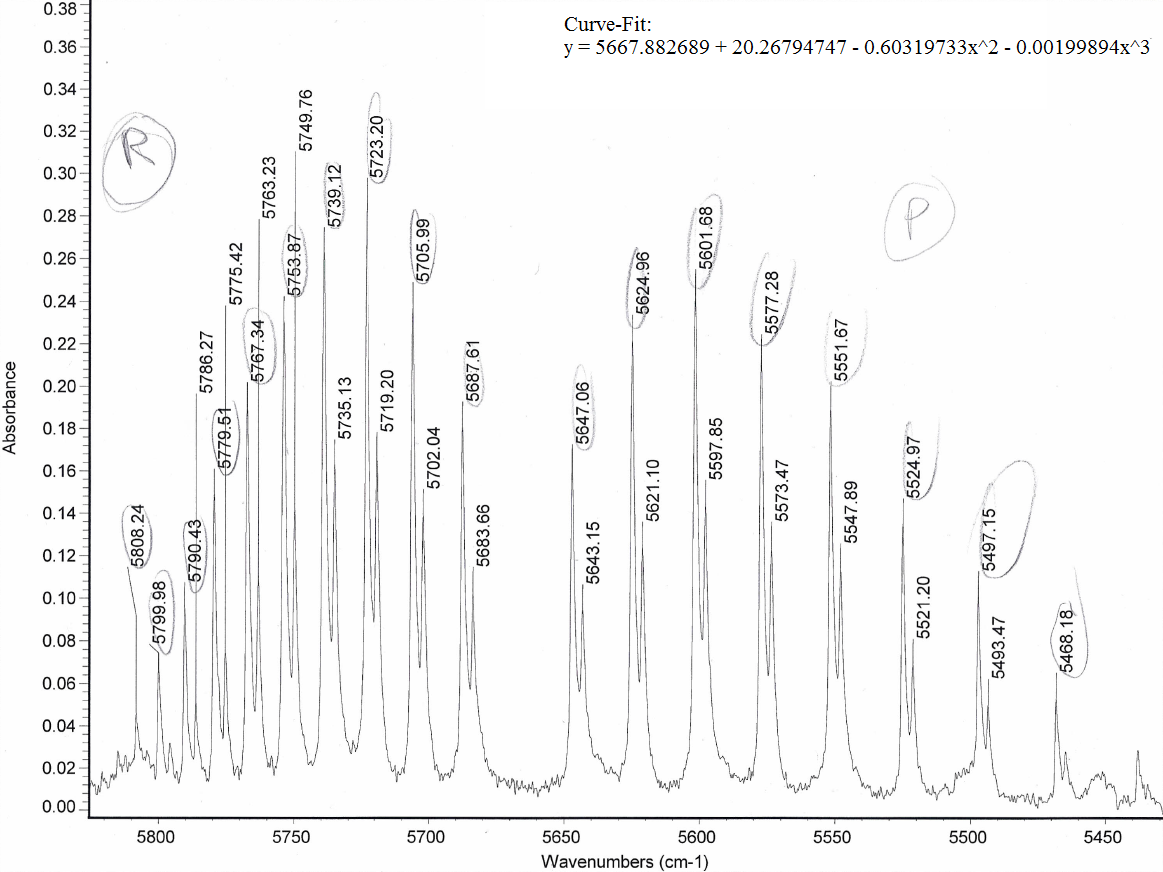 HCl Overtone/Forbidden Transitions The ro-vibrational IR spectrum of HCl in a viewable range for the overtone transitions. The ones visible here are P(1) through P(8) and R(0) through R(9), and the taller peaks were circled.
HCl Overtone/Forbidden Transitions The ro-vibrational IR spectrum of HCl in a viewable range for the overtone transitions. The ones visible here are P(1) through P(8) and R(0) through R(9), and the taller peaks were circled.
Naturally, we would expect the lower frequencies to be more separated than the higher frequencies because the anharmonic oscillator model (the realistic, nonideal model) has energy level spacings that converge eventually (whereas the harmonic oscillator model, the ideal model, has equal energy level spacings).
The curve fit equations basically graph P-and-R-branch integer spacings with peak separations

