How can vectors be parallel?
1 Answer
Sep 5, 2014
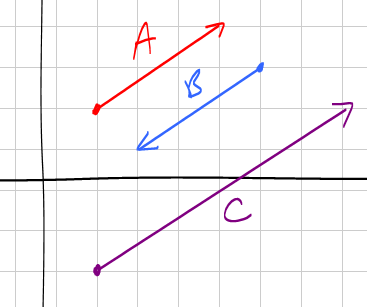
So,
First, notice that they don't have to point in the same direction.
Second, notice that they don't have to have the same magnitude.
Although these vectors are drawn in different places, vectors are positionless. We draw them in different positions just so that we can see them easier. We can draw them all at the origin and the vectors would still be the same.
We can algebraically check that they are parallel by comparing the slopes, in this case, they are all
If the vectors are in 3D, you can't compare the slopes. You would have to perform an operation called a cross product and check that the cross product equals

