How can you find the intersection of two lines?
1 Answer
Method 1: Graphically
Example: Find the point of intersection for the following two lines:
My preference for graphing lines is to write in slope intercept form,
Written in this form, the equations are:
#y = 5 - x#
#y = 1 - 3x#
So you have slope of
If we graph these two lines, we should get something like the following.
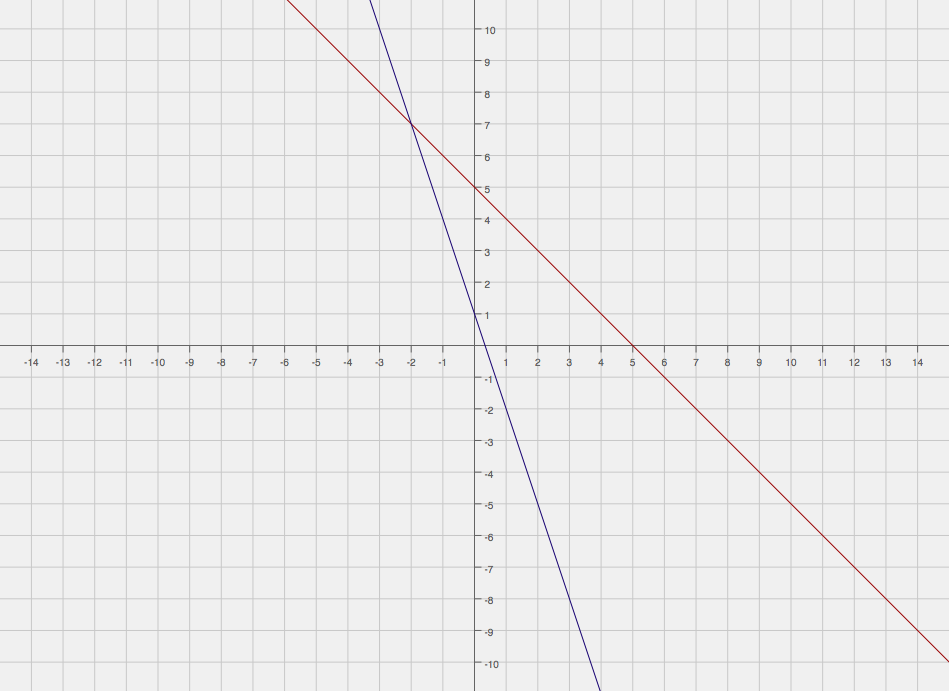
Which has intersection point
Method 2: Algebraically
There are two methods of doing this:
•Substitution
•Elimination
Example: Solve the following system through substitution:
The substitution method involves substituting one equation into the other, thus eliminating to one variable.
Note that from the first equation we can easily obtain
#2(5 - 3y) - 3y = -8#
#10 - 6x - 3y = -8#
#-9y = -18#
#y = 2#
We can see by substitution that
#x + 3(2) = 5 -> x = -1#
Therefore, the solution to the given system is
Example: Solve the following system through elimination:
We often use elimination when there is no variable that is easy to isolate. Note that all of the variables in the above system have coefficients
Let's try to multiply both sides of the first equation by
#-2(2x - 3y) = -2(12) -> -4x + 6y =- 24#
If we add the two equations now, we get:
#0x + 11y = -22#
#y = -2#
Solve for
#2x - 3(-2) = 12 -> 2x = 6 -> x = 3#
Therefore, the solution to the given system is
Practice Exercises
#{(2x + y = 13), (x - 3y = -11):}#
#{(3x -3y = 21), (5x + 12y = 18):}#
#{(4x + 5y = -4), (3x + 7y = -16):}#
Solutions
Hopefully this helps, and good luck!

