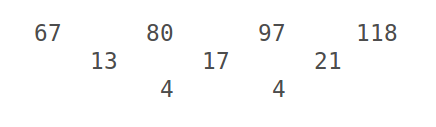Since the #y# values are given for #x=1, 2, 3, 4# let us write the #y# values as a sequence, then form the difference of those terms, then the difference of the differences...
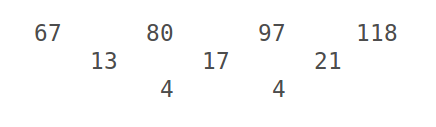
Notice that it takes #2# steps to get to a constant sequence, so this is a quadratic.
Next, let us construct the #y# value for #x=0# by adding in a column on the left...

We do this by writing in another #4# on the last row, then calculating #9# as #13 - 4#, then calculating #58# as #67 - 9#.
Now we have added this row for #x=0# we can use its values to find the equation of the quadratic...
#f(x) = color(red)(58) + color(red)(9) * (x)/(1!) + color(red)(4) * (x(x-1))/(2!)=58+7x+2x^2#
#=2x^2+7x+58#