How did earlier mathematicians calculate limits so accurately?
Especially things like how #lim_(x->0)# #(sinx^@/x^@)=sin1# but #lim_(x->0)# #(sinx^"rad"/x^"rad")=1#
Especially things like how
1 Answer
With the exception of using L'Hospital's Rule and Taylor Series (which both rely on Calculus) they would use the same techniques that we currently use.
Most notably is that the limit you have used as an example, which can easily be derived using basic geometry.
Example
This is a technique used by Archimedes circa 250BC where he used regular polygons inside and outside to obtain approximations for
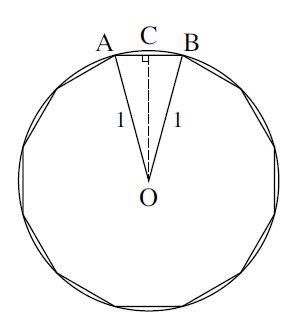
The above figure shows a regular
Now,
# 360^o div 12 = 30^o => hat(AOB) = 30^o #
# C# is the midpoint of#AB => AB=2BC #
# :. COB =15^o#
By trigonometry we have:
# sin hat(COB)=(BC)/1 #
But#AB=2BC# and#hat(COB)=15^o => sin 15^'=1/2AB#
# :. AB = 2sin15^o #
Using
# cos 30^o = 1-2sin^2 15^o #
# :. sqrt(3)/2 = 1-2sin^2 15^o #
# :. 2sin^2 15^o = 1-sqrt(3)/2#
# :. sin^2 15^o = (1-sqrt(3)/2)/2#
# :. sin^2 15^o = (2-sqrt(3))/4#
# :. sin 15^o = 1/2sqrt(2-sqrt(3) #
Then he calculated the perimeter of the polygon using:
# P = 12AB #
# \ \ \ = 24sin 15^o #
# \ \ \ = 12 sqrt(2-sqrt(3) #
Then as above:
Circumference of circle
#gt # perimeter of polygon
# :. (2pi)(1) gt 12 sqrt(2-sqrt(3) #
# :. pi gt 6 sqrt(2-sqrt(3) # ..... [A]
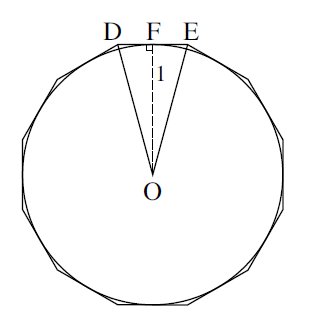
Next Archimedes considered a 12-sided polygon that lies outside a circle of radius
As before,
# hat(DOE) = 30^o => hat(FOE)=15^o #
And,#DE=2FE#
By trigonometry:
# tan hat(FOE)=(FE)/1 #
But#DE=2FE# and#hat(FOE)=15^o => tan15^o=1/2 \ DE #
Using
# tan 30^o = (2tan15^o)/(1-tan^2 15^o) #
# :. 1/sqrt(3) = (2t)/(1-t^2) # , where#t=tan 15^o #
# :. 2sqrt(3)t = 1-t^2 #
# :. t^2+2sqrt(3)t-1 = 0 #
This is quadratic in
# t = (-2sqrt(3) +- sqrt(2sqrt()^2-4(1)(-1)) ) /2 #
# \ \ = -sqrt(3) +- 2 #
But as#t=tan 15^o > 0 => tan 15^o = 2-sqrt(3) #
And so the perimeter of this polygon is:
# P = 12 DE #
# \ \ \ = 12 tan 15^o #
# \ \ \ = 24(2-sqrt(3)) #
This time:
Circumference of circle
#lt # perimeter of polygon
# :. (2pi)(1) lt 24(2-sqrt(3)) #
# :. pi lt 12(2-sqrt(3)) # ..... [B}
Combining the results [A] and [B} Archimedes then showed that:
# 6 sqrt(2-sqrt(3)) lt pi lt 12(2-sqrt(3)) #
# :. 3.10582 ... lt pi lt 3.21539 ... #
# :. 3.106 lt pi lt 3.215 #
And of course we know that:
# 3.141592653589793238462 ... #
Archimedes used this same technique on a
As we take larger and larger