How did the Hooke’s law help IR in the position of absorption bands?
1 Answer
The relevance of Hooke's law is that it is a ball-and-spring model, the basis for the harmonic oscillator, which is the name for the simplified, ideal diatomic that models molecular vibrations.
IR spectroscopy graphs the intensities of molecular vibrations versus their frequencies in wavenumbers (
You may have vibrations (or more formally, "vibrational modes") like the following:
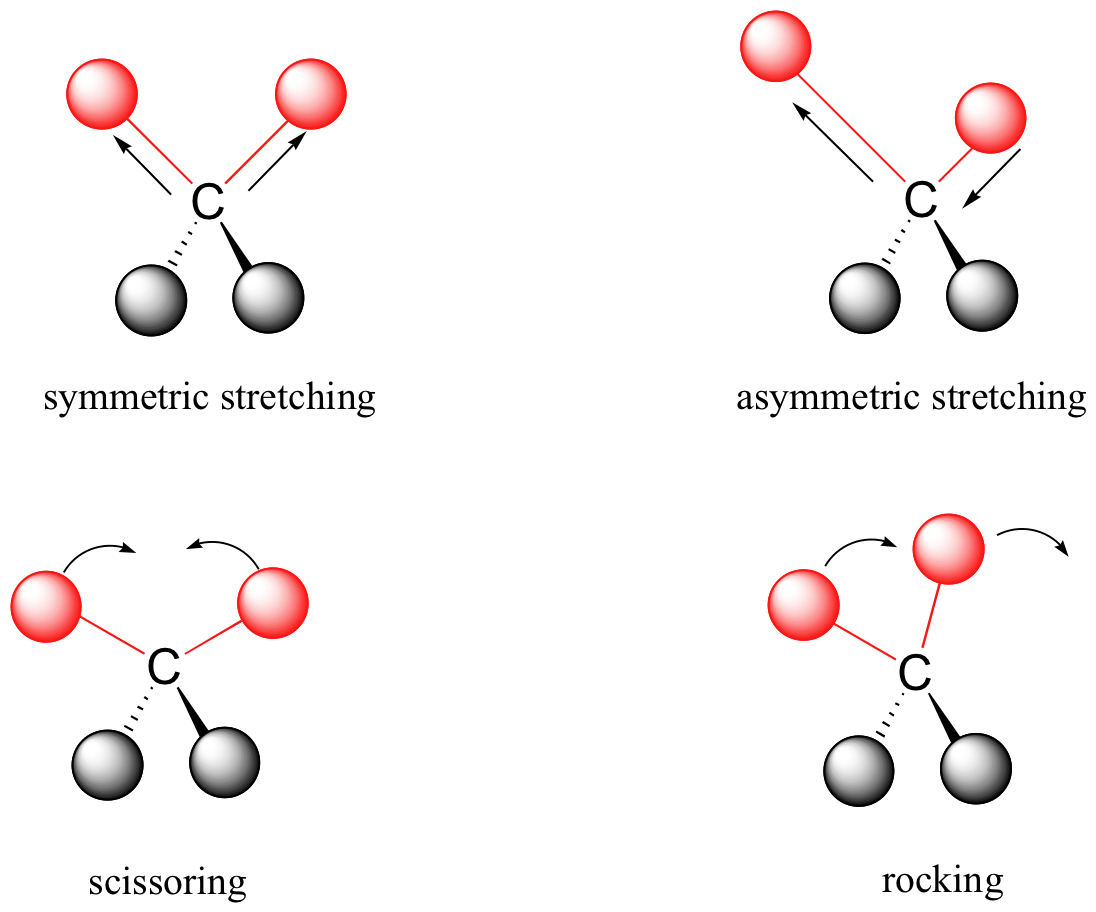 http://chemwiki.ucdavis.edu/
http://chemwiki.ucdavis.edu/
Bends (such as scissoring and rocking) are weaker than stretches (such as symmetric and asymmetric stretching), and the weaker vibrations show up at lower frequencies. You can see so here with methane's vibrational frequencies.
You can see that the bends have less motion and therefore imply lesser energetics, and stretches have more motion and imply greater energetics, which visually demonstrates why stretches show up at higher frequencies.

