Question

How do find the vertex and axis of symmetry, and intercepts for a quadratic equation `y=x^2 +2x -5`?

Answer 1

The vertex is at (`-1,-2`).
The axis of symmetry is `x = 1`.
The `y`-intercept is at (`0,5`).
The `x`-intercepts are at `x = -1- sqrt6` and `x = -1 + sqrt 6`.

Explanation:

The standard form for the equation of a parabola is

`y= a^2 + bx +c`

Your equation is

`y = x^2 + 2x - 5`

So

`a = 1`, `b = 2`, and `c = 5`.

Vertex

Since `a > 0`, the parabola opens upwards.

The `x`-coordinate of the vertex is at

`x = –b/(2a) = -2/(2×1) = -2/2 = -1`.

Insert this value of `x` back into the equation.

`y = x^2 + 2x - 5 = (-1)^2 + 2(-1) - 5 = 1 - 2 - 5 = -6`

The vertex is at (`-1,-2`).

Axis of symmetry

The axis of symmetry must pass through the vertex, so

The axis of symmetry is `x = -1`.

`y`-intercept

To find the `y`-intercept, we set `x = 0` and solve for `y`.

`y = x^2 + 2x – 5 = 0^2 + 2×0 -5 = 0 + 0 – 5 = -5`

The `y`-intercept is at (`0,5`).

`x`-intercepts

To find the `x`-intercepts, we set `y = 0` and solve for `x`.

`y = x^2 + 2x – 5`

`0 = x^2 + 2x – 5`

`x = (-b ±sqrt(b^2-4ac))/(2a)`

`x = (-2 ± sqrt(2^2 - 4×1×(-5)))/(2×1)`

`x = (-2 ± sqrt(2^2 - 4×1×(-5)))/(2×1)`

`x = (-2 ± sqrt(4 + 20))/2`

`x = (-2 ± sqrt24)/2`

`x = -1 ± 1/2sqrt24`

`x = -1 ± 1/2(sqrt(4×6))`

`x = -1 ± 1/2(2sqrt6)`

`x = -1 ± sqrt6`

The `x`-intercepts are at `x = -1- sqrt6` and `x = -1 + sqrt 6`.

Graph

Now we prepare a chart.

The axis of symmetry passes through `x = -1`.

Let's prepare a table with points that are 5 units on either side of the axis, that is, from `x = -6` to `x = 4`.

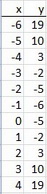
Plot these points.

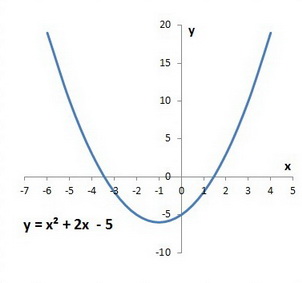
And we have our graph.